题目描述
内存是计算机重要的资源之一,程序运行的过程中必须对内存进行分配。
经典的内存分配过程是这样进行的:
1、 内存以内存单元为基本单位,每个内存单元用一个固定的整数作为标识,称为地址。地址从0开始连续排列,地址相邻的内存单元被认为是逻辑上连续的。我们把从地址i开始的s个连续的内存单元称为首地址为i长度为s的地址片。
2、 运行过程中有若干进程需要占用内存,对于每个进程有一个申请时刻T,需要内存单元数M及运行时间P。在运行时间P内(即T时刻开始,T+P时刻结束),这M个被占用的内存单元不能再被其他进程使用。
3、假设在T时刻有一个进程申请M个单元,且运行时间为P,则:
- 若T时刻内存中存在长度为M的空闲地址片,则系统将这M个空闲单元分配给该进程。若存在多个长度为M个空闲地址片,则系统将首地址最小的那个空闲地址片分配给该进程。
- 如果T时刻不存在长度为M的空闲地址片,则该进程被放入一个等待队列。对于处于等待队列队头的进程,只要在任一时刻,存在长度为M的空闲地址片,系统马上将该进程取出队列,并为它分配内存单元。注意,在进行内存分配处理过程中,处于等待队列队头的进程的处理优先级最高,队列中的其它进程不能先于队头进程被处理。
现在给出一系列描述进程的数据,请编写一程序模拟系统分配内存的过程。
输入格式
第一行是一个数N,表示总内存单元数(即地址范围从0到N−1)。
从第二行开始每行描述一个进程的三个整数T、M、P(M≤N)。
最后一行用三个0表示结束。
数据已按T从小到大排序。
输入文件最多10000行,且所有数据都小于109。
输入文件中同一行相邻两项之间用一个或多个空格隔开。
输出格式
输出包括2行。
第一行是全部进程都运行完毕的时刻。
第二行是被放入过等待队列的进程总数。
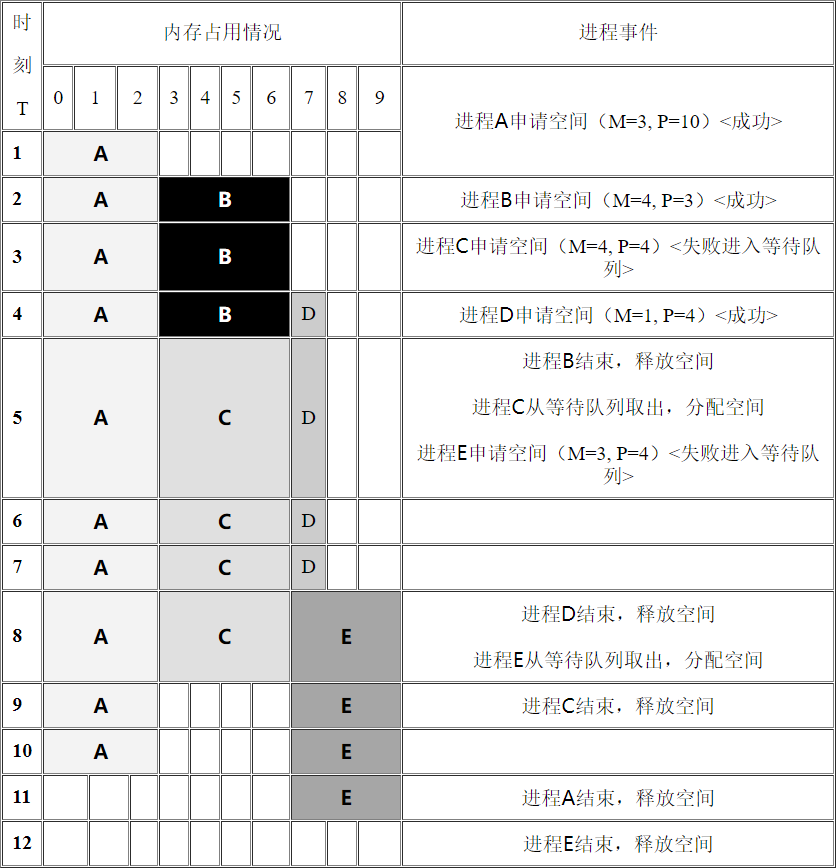
输入样例:
10
1 3 10
2 4 3
3 4 4
4 1 4
5 3 4
0 0 0
输出样例:
12
2
提示
题意理解
这道题目的题目描述特别特别长,看的人脑袋痛,博主尽量精简.
首先题目中有很多进程,每一个进程它都有t,m,p三个表示,表示这个进程在第T时刻开始申请要使用内存,而且要使用长度为M的连续内存地址,然后这段内存要花费P个时间.
举个例子T=1,M=2,P=3.表示第一秒的时候,我们申请要使用内存,然后要一段长度为2的连续内存地址段,要求使用三秒钟.使用完后会自动释放掉.
对于每一个申请的进程而言,有两种情况.
| 情况 | 先决条件 | 处理方式 |
|---|---|---|
| 可以存储 | 在当前空闲内存中存在一个长度为M的连续空闲内存 | 找到满足条件的空闲内存中,地址开头最小的地址 |
| 不可以存储 | 不存在一个长度为M的连续空闲内存 | 加入候选队列的队尾,且如果任意时刻,候选队列的队头可以存储,那么立即存储. |
算法详细
这道题目的算法,题目中很明显的告诉我们了是一道模拟题目.博主将题目描述的暗示已经加黑了.
这道题目的模拟,非常有特色,因为统统都是在数据结构上进行的模拟,我们来一步步地剖分这道题目,就像树链剖分的轻重链剖分一样.
在这道题目有很多要点,我们先来列个大纲康康.
首先这道题目有两种关键性的操作,那就是使用(插入)操作和释放(删除)操作.
对于使用操作而言,我们可以通过以下这个数据结构达成目标.
如果说我们可以存储当前进程的话,那么显然有两种情况.
- 当前内存表中本来就存在一个长度为M的空闲内存
- 我们经过了删除操作,使得内存表中出现了一个长度为M的空闲内存.
我们可以将内存表看作是一个区间,那么对于这个区间而言,那么显然每一个占用内存的进程,就是一个阻碍物.我们来一个图片来揭示真相.

Hint:红色部分为占用内存,白色部分为空闲内存.下文都以红色白色代替.
我们发现,一段连续的白色部分可以表示为,第i个红色部分的结尾处到第i+1个红色部分的开头.
这里特别注意以下,我们要处理边界,可以将−1处染成红色,n处染成白色.请记住这里的内存表,是[0,N−1]
根据上面的表示,我们的图片就变成下图所示.

所以说我们这道题目就可以用双向链表处理了,来保存每一段红色部分,最后取存储白色部分,不过呢,我们使用STL的大佬们,肯定会想到一个点,那就是我们可以使用Set(平衡树)数据结构来达到我们的目的.
Hint:平衡树,具有排序性质,资瓷O(log)级别的插入,删除,求前驱,求后继等操作.是一款强大的数据结构
既然我们的使用操作都完成完毕了,那么接下来就是我们的释放操作的处理.
释放操作,也就是释放第T时刻的时候,已经完成的进程.
首先我们要确定一个点,就是释放每一个内存段,实际上就是将它从我们的Set里面删除.
所有的可以是释放的内存段都释放完毕后,我们再从等待的队列中取出队头,判断能否将队头成功加入即可.
还有我们的释放的顺序要保持.
代码实现
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
int n,cnt,t,m,p,ans;//ans:全部进程都运行完毕的时刻,cnt:被放入过等待队列的进程总数
queue<PII> waits; //等待队列,first: 内存长度,second: 占用时间
set<PII> runs; //当前进程,first: 起始下标,sercond:长度
priority_queue<PII, vector<PII>, greater<PII>> endts; //小根堆,维护释放顺序,first: 释放时间,second: 起始下标
bool give(int t, int m, int p)
{
for(auto it=runs.begin();it!=runs.end();it++)//扫描所有的红色部分
{
auto jt=it;
jt++;//jt相当于i+1,it相当于i
if (jt!=runs.end())
{
int start=it->first+it->second;
if (m<=jt->first-start)//如果说本空余内存段满足条件
{
runs.insert({start,m});//加入
endts.push({t+p,start});//记录下来
return true;
}
}
}
return false;
}
void finish(int t)
{
while (endts.size() && endts.top().first<=t)//判断小根堆顶的进程(结束时间最早的)是否能结束
{
int f=endts.top().first;
while (endts.size() && endts.top().first==f)////可能有多个结束进程时间相同的进程
{
auto top=endts.top();
endts.pop();//出堆
auto it=runs.lower_bound({top.second, 0});
runs.erase(it);
}
ans=f;//更新
while (waits.size())//检查等待队列的队首是否能安排
{
auto front=waits.front();//等待的队头
if (give(f,front.first,front.second))//可以放入
waits.pop();
else
break;
}
}
}
void init()
{
ios::sync_with_stdio(false);
cin>>n;
runs.insert({-1, 1}),runs.insert({n, 1});//边界处理
while (cin>>t>>m>>p,t || m || p)
{
finish(t);//先释放,确保剩余内存最大化.
if (!give(t,m,p))//不可以加入
{
waits.push({m,p});//等待队列欢迎你
cnt++;//记录,题目的计划二
}
}
finish(2e9);//你可以认为全部释放.
cout<<ans<<endl<<cnt<<endl;
}
int main()
{
init();
return 0;
}
Hint:感谢Hz叔的代码注释


这个时间复杂度怎么保证啊,感觉是n方的?
每次判断能不能插入都要遍历一遍吧?
10000*10000能过
if (!give(t,m,p))应该要改成if(!waits.empty()||!give(t,m,p))吧,因为等待队列的优先级更高,如果等待队列在释放t后非空,就不能考虑现在的进程吧。
不会吧?Hz叔的注释不会出锅ba。。。
好像是我对题意有点误解
秀啊,比我看到过的代码短了好多
QwQ
orzorz
OTZ