y氏dp分析法

• 状态表示：

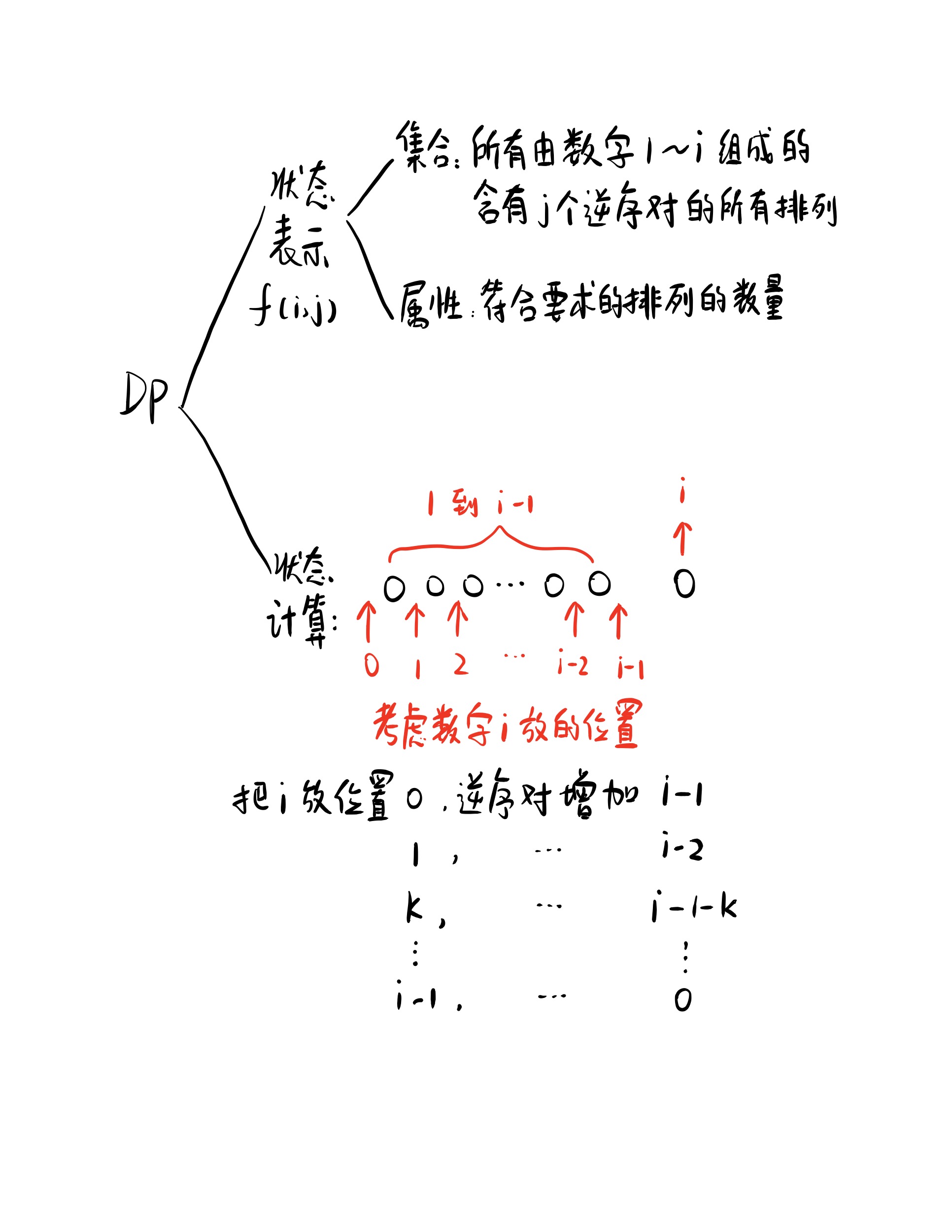
集合：f(i, j)表示所有由数字1~i组成的含有j个逆序对的排列

属性：符合上述要求的排列的数量

• 状态计算：

考虑最后一个数字i所放的位置，由于前面已经排列有数字1~i-1，故数字i可放在下图0~i-1共i种位置处。由于数字i是最大的数字，于是如果放在0处，则会增加i-1个逆序对，放在1处，会增加i-2个逆序对…k处…i-1-k个逆序对…i-1处…0个逆序对。

所以当前状态的转移方程为从1~i-1个数选，所有可能逆序对数量下的排列数量之和。

f(i,j) =                  f(i-1,j-i+1) + f(i-1,j-i+2) + ... + f(i-1,j-1) + f(i-1,j-0)

f(i,j - 1) = f(i-1,j-i) + f(i-1,j-i+1) + f(i-1,j-i+2) + ... + f(i-1,j-1)

• 当我们从小到大枚举j时，我们发现对于每一个f(i,j)，其实较f(i,j-1)来说多了一项f(i-1,j-i),少了一项f(i-1,j)

注意：当j<=i-1时，j-i+1<=0，因此此时的状态转移方程里是没有f(i-1,j-i+1)这一项甚至更多，更形象地理解就是当前状态中逆序对数量为小于i-1时，数字i就不能放在位置0或靠前的一些位置上,因为此时较上一状态逆序对的增加量已经超过i-1了。所以说当j<=i-1时，逆序对增加的数量最多为j，此时状态转移方程变为

f(i,j) = f(i-1,0) + f(i-1,1) + ... + f(i-1,j-1) + f(i-1,j)

所以通过分析，只有当j>i时，我们才需要减去项f(i-1,j-i)。也可以理解为每一个状态转移方程都有j项之和，所以每一次状态转移都需要加一项减一项来维持项数。但是当j<=i-1时，状态转移方程中项数还不满这么多，所以不需要减去某项。

在代码中我们用s来表示状态转移方程中的这一段和

代码

class Solution {
public:
    int kInversePairs(int n, int k) {
        vector<vector<int>> f(n + 1, vector<int> (k + 1));
        const int MOD = 1e9 + 7;
        f[1][0] = 1;
        for (int i = 2; i <= n; i ++) {
            long long s = 0;
            for (int j = 0; j <= k; j ++) {
                s += f[i - 1][j];
                if (j >= i) s -= f[i - 1][j - i];
                f[i][j] = (s + MOD) % MOD;
            }
        }
        return f[n][k];
    }
};