直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

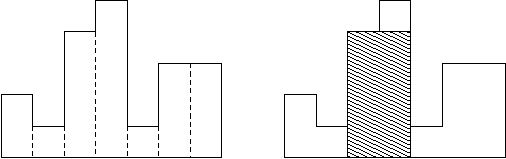
例如，图例左侧显示了由高度为2,1,4,5,1,3,3的矩形组成的直方图，矩形的宽度都为1：

通常，直方图用于表示离散分布，例如，文本中字符的频率。

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

输入格式

输入包含几个测试用例。

每个测试用例占据一行，用以描述一个直方图，并以整数n开始，表示组成直方图的矩形数目。

然后跟随n个整数$h_1，…，h_n$。

这些数字以从左到右的顺序表示直方图的各个矩形的高度。

每个矩形的宽度为1。

同行数字用空格隔开。

当输入用例为n=0时，结束输入，且该用例不用考虑。

输出格式

对于每一个测试用例，输出一个整数，代表指定直方图中最大矩形的区域面积。

每个数据占一行。

请注意，此矩形必须在公共基线处对齐。

数据范围

$1≤n≤100000,$
$0≤h_i≤1000000000$

输入样例：

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

输出样例：

8
4000

题目题解

很显然，这是一道单调栈的经典例题,但是我们使用悬线法也是能写的

想了解悬线法？ 集训队论文

我们通过画样例可以轻松的得到，我们需要算出当前高度能拓展到最长的左区间和右区间在哪里

那么一定有，左区间的所有高度都比当前高度高，右区间的所有高度都比当前高度高

这类问题我们可以分开考虑，先考虑左边，再考虑右边，但是一个一个考虑需要$n^2$ 如何更快？

可以通过单调栈进行优化，这样就能变成$O(n)$的复杂度了

我们考虑一个栈，栈的元素一定是单调的，进来的数如果让栈不符合单调性，那么就吐出栈中的元素，然后放新来的数
那么此题，我们要维护的就是一个单调递增的栈

如果一个数大于栈顶元素，那么它一定满足大于栈内的所有元素
同理，如果小于，那么就一定满足小于栈内的所有元素

如果进来一个新数，这个数是小于栈顶元素的，那么就将栈顶取出，直到栈内元素为空或者栈顶元素小于此元素
有何意义？此时我们的左区间一定是栈顶元素的下标，那么这样我们就能进一步得出，我们维护的是一个单调递增的栈的下标，同理，右区间也可同样得出，这样通过计算即可得到答案。

但是，我们进一步可得到，如果栈内元素为空的话，我们的左区间就是第一位数，还要特判，比较麻烦
我们可以先在第0号位放一个-1，那么我们的左区间就是0 + 1号位了。

详细看代码

//#define fre yes

#include <stack>
#include <cstdio>
#include <iostream>
#include <algorithm>

std::stack<int> s;

const int N = 100005;
int f[N], l[N], r[N];

int n;
void Get(int bound[]) { //单调栈
    f[0] = -1; //加一个常用处理
    s.push(0); //先把第零号位的下标放进去
    for (int i = 1; i <= n; i++) {
        while(!s.empty() && f[s.top()] >= f[i]) s.pop(); //栈内必须满足单调性
        bound[i] = s.top() + 1; //得到X区间
        s.push(i); //再将新数放进去
    }
}

int main() {
    while(scanf("%d", &n), n) {
        for (int i = 1; i <= n; i++) {
            scanf("%d", &f[i]);
        }

        Get(l); //得到左区间
        std::reverse(f + 1, f + 1 + n); //将数组翻转，这样我们就只用写一个函数了
        Get(r); //得到右区间

        long long ans = 0;
        for (int i = 1, j = n; i <= n; i++, j--) {
            ans = std::max(ans, f[i] * (n + 1 - l[j] - r[i] + 1ll));
            // 这里要拆开看
            //设x = n + 1 - l[j]
            //设y = r[i]
            //x的含义就是，因为当前我们是已经翻转的数组，所以我们要得到l的真实下标
            //y的含义就是 （字面意思）
            //x - y + 1的含义就是整个长的长度
        } printf("%lld\n", ans);
    } return 0;
}