在 $\text{Luogu}$ 上的地址:click here
浅谈遗传算法
由于网上遗传算法的博客要么是例题不足,要么是过于工程化,所以准备写一篇更加亲民的博客。篇幅不长,深入浅出。由于笔者能力有限,可能出现部分错误。
什么是遗传算法
就不从百度上往下搬了。
遗传算法,又称为 $\text{Genetic algorithm(GA)}$。其主要思想就是模拟生物的遗传与变异。它的用途非常广泛,可以用于加速某些求最大或者最小值的算法。
特别提醒,遗传算法是一个随机算法,会有一定的错误概率。
遗传算法前置知识
首先先来补充一些生物知识:
每个生物都有许许多多的染色体,这些染色体呈棒状。每个染色体都由双螺旋状的 $\text{DNA}$ 和蛋白质构成。每条 $\texttt{DNA}$ 上都有许多基因。放个图来理解一下。
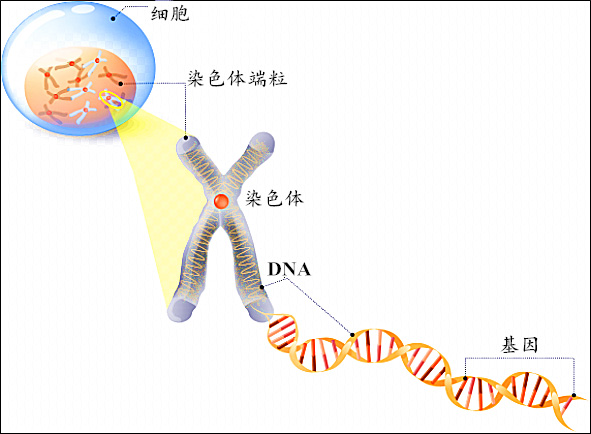
大概不需要过多解释,中学生物都学过。将 个体,染色体,基因 范围由大到小排序为 :
个体(Individual) > 染色体(chromosome) > 基因(gene)
遗传算法模拟了自然选择的过程。那些适应环境的个体能够存活下来并且繁殖后代。那些不适应环境的个体将被淘汰。换言之,如果我们对每个个体都有一个适应度评分(用来评价其是否适应环境),那么对于适应度高的物体来说,将具有更高的繁殖和生存的机会。
另外,为了保持种族的稳定性,我们会将父代的基因传递下去。
遗传算法基础
遗传算法基于一些不证自明的理论依据:
- 种群中的个体争夺资源和交配。
- 那些成功的(最适合的)个体交配以创造比其他人更多的后代。
- 来自 “最适” 父母的基因在整个世代中传播,即有时父母创造的后代比父母任何一方都好。
- 因此,每一代人都更适合他们的环境。
遗传算法基础概念
拿古代人类来举例子:
- 个体($\text{Individual}$):每个生物。即每个古人类个体。
- 种群($\text{population}$):一个系统里所有个体的总称。比如一个部落。
- 种群个体数($\text{POPULATION}$):一个系统里个体的数量。比如一个部落里的人数。种群个体数通常与生物多样性有关,即种群个体数过少可能导致过快收敛或早熟。
- 染色体($\text{chromosom}$):每个个体均携带,用来承载基因。比如一条人类染色体。
- 基因($\text{Gene}$):用来控制生物的性状(表现)。
- 适应度($\text{fitness}$):对某个生物是否适应环境的定量评分。比如对某个古人类是否强壮进行 $[1, 100]$ 的评分。
- 迭代次数($\text{TIMES}$):该生物种群繁衍的次数。比如古人类繁殖了 $100$ 万年。你可以自己设置迭代次数。
一定要记住这些英文名字!!!,后面会经常用到
配图表示:
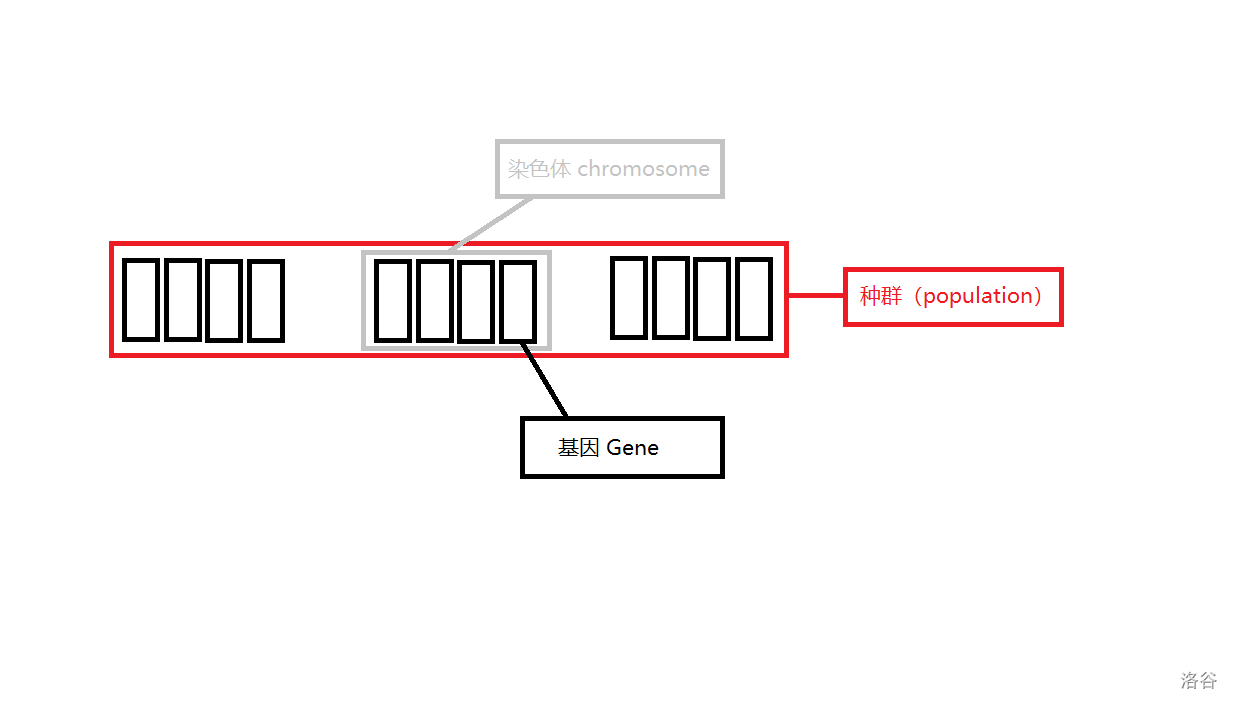
图中,种群、染色体、基因都已经标注上了。种群个体数量为 $3$,每个个体都是染色体 $+$ 对应的适应度。
在算法中,我们对每个个体计算其染色体的适应度($\text{fitness}$)来决定它是否优秀。
小试牛刀
尝试构建一个名字叫做 $\text{Individual}$ 的结构体,里面存储一个个体的信息。可以自己尝试先写一下。
参考答案:
struct Individual {
string chromosome; // 染色体
int fitness; // 个体的适应度
Individual(string chromosome); // 初始化
int calc_fitness(); // 计算适应度
Individual mate() // 即交叉算子(CrossOver)。后面会讲到。
Individual mutation() // 即变异算子(Mutation)。后面会讲到。
};
Individual(string chromosome) {
this -> chromosome = chromosome;
this -> fitness = calc_fitness();
}
遗传算法算子
1.交叉算子($\text{CrossOver}$)
也有将该算子称为 $\text{mate}$ 的。我更倾向于第二种叫法,因为第二种字数更少。
交叉算子就是模拟父母双方交配过程。想一想人类交配时,每个基因会随机的来自父亲或者母亲。我们可以模拟这个过程。假设我们的染色体用 $\text{string}$ 存储,可以实现下面的交配代码:
// par 代表母亲,chromosome 代表父亲(即本身)的染色体,par.chromosome 则代表母亲染色体。
Individual Individual::mate(Individual par) { // 交叉
string child = ""; // 子代染色体
int len = chromosome.size();
for (int i = 0; i < len; i ++ ) {
double p = random(0, 100) / 100; // 计算来自父母的概率
if (p <= 0.5) child += chromosome[i]; // 一半概率来自父亲
else child += par.chromosome[i]; // 另一半来自母亲
}
return Individual(child);
}
当然,你也可以思考一些其他的交叉思路,比如随机抽取某些段进行交换。如下图所示:
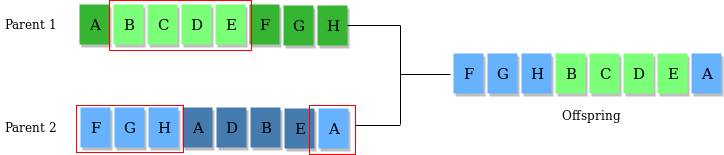
(以上图片来自Genetic Algorithms)
这种算法通常在二进制条件下更加实用。
2.变异算子($\text{mutation}$)
即低概率地随机地改变某个基因。这样可以有效避免程序陷入局部最优或者过慢收敛。例如:
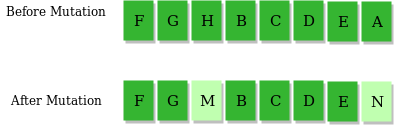
一般来说,我们可以设计一个变异概率。变异率大概在 $0.01 \sim 0.05$ 之间最优。变异率太高会导致收敛过慢,变异率太低则会导致陷入局部最优。
遗传算法策略
- 精英保留策略
还是拿古人类举例。假设我们是上帝,我们想要古人类实现长久发展,最好的办法就是尽可能的将那些头脑敏捷,肢体强壮的个体保留下来,淘汰那些老弱病残的个体。
在程序中,我们将个体按照适应度排序,把适应度最好前 $k \%$ 的保留下来,剩下的随机交配。通常,$k$ 可以设成 $1 \sim 20$。设置太高则会局部最优,太低则会收敛过慢。也可以直接选定将前 $k$ 个保留。
- 概率保留策略
学名好像是 Stoffa改进方法,这不重要。总之,就是为了避免父母生出傻孩子浪费时间,把傻孩子(适应度低的后代)直接抛弃。
假设我们要求收敛到最低适应度,后代适应度为 $y$,父代适应度为 $x$,有 $\Delta = y - x$。若 $\Delta < 0$,证明子代比父代更好,我们一定接受。对于 $Delta > 0$,证明子代不如父代好,我们以一定概率接受。之所以要有一定概率接受,是为了避免出现局部最优解。
这个概率我们怎么来算呢?有一种方法给出了概率的计算函数:
$$P(\Delta) = e ^ { - \Delta / t}$$
其中 $t$ 是我们设定的参数值,一般随着迭代次数增大而减小。如果 $P(\Delta) > \operatorname{rand}(0, 1)$,那么我们就接受它。
为什么是 $- \Delta$ 呢?因为 $\Delta > 0$,我们要保证 $e^x$ 小于 $1$ 才能保证部分接受。因此要用 $- \Delta$。
为什么要用 $e ^ x$ 呢?我不知道,大概是因为它的积分等于原函数吧。。。
下面放一张遗传算法求最短哈密尔顿路径的收敛图像。其中绿色实线是加了概率函数的,蓝色虚线则没有加。可以看出,绿色实现收敛的比较快,侧面证明了 Stoffa改进方法 的正确性。
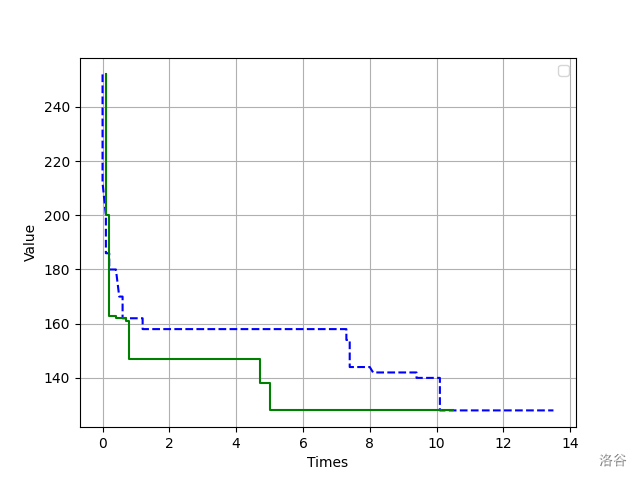
思考题
如果我们要求最大适应值,那么概率的计算函数应当怎么计算呢?
答案:$P(\Delta) = e ^ {\Delta / t}, Delta < 0$ 。
例题
例题 1 : 牛刀小试
给定一个目标字符串($\text{target}$),目标是从相同长度的随机字符串开始生成目标字符串。
比如从 $\texttt{114514QAQ}$ 生成 $\texttt{123456789}$。
这里先讲一下适应度函数的构造方法:比较当前染色体与目标字符串之间不同的字符个数即为适应度。显然,适应度越低越好。
上面都已经讲过了,这里直接贴出代码:
全部代码:
请点这里。
看一下输出结果:
Generation: 0 String : "'IalP?= VX_ Fitness : 10
Generation: 1 String : 9'ne;2.S JA{ Fitness : 9
Generation: 2 String : kvT W 1j!t! Fitness : 8
Generation: 3 String : kvT W{1j!t! Fitness : 8
Generation: 4 String : 'vT W 1j!t! Fitness : 7
Generation: 5 String : Idve Y{vIqt! Fitness : 6
Generation: 6 String : I=ve7r;t nt! Fitness : 5
Generation: 7 String : I've W 1jit! Fitness : 4
Generation: 8 String : I've W 1jit! Fitness : 4
Generation: 9 String : I'vT W t it! Fitness : 3
Generation: 10 String : I'vT W t it! Fitness : 3
Generation: 11 String : I've W t it! Fitness : 2
Generation: 12 String : I've g 1 it! Fitness : 2
Generation: 13 String : I've g t it! Fitness : 1
Generation: 14 String : I've g t it! Fitness : 1
Generation : 15 String : I've got it! Fitness : 0
怎么样,有没有感受到遗传算法的强大!
例题 2
题目描述
糖果店的老板一共有 $M$ 种口味的糖果出售。为了方便描述,我们将 $M$ 种口味编号 $1$ ∼ $M$。
小明希望能品尝到所有口味的糖果。遗憾的是老板并不单独出售糖果,而是 $K$ 颗一包整包出售。
幸好糖果包装上注明了其中 $K$ 颗糖果的口味,所以小明可以在买之前就知道每包内的糖果口味。
给定 $N$ 包糖果,请你计算小明最少买几包,就可以品尝到所有口味的糖果。
我知道可以用状压,但是这道题还可以用遗传!
考虑将品尝每包糖果的顺序作为染色体,适应度即为品尝过所有糖果需要购买的糖果包数的最小值。(这里指从头往后取)
注意,这里的适应度计算函数需要特别处理。由于染色体是个排列,我们直接交叉肯定会出现单个染色体内有许多基因重复。因此考虑“自交”,即用更高的变异概率代替双亲交配。
核心代码在这里:
#define POPULATION 1000
#define TIMES 10
using namespace std;
const int N = 110, M = 21;
int a[N][M], n, m, K, ans = 0x3f3f3f3f;
int random(int l, int r) {
return rand() % (r - l + 1) + l;
}
struct Individual {
vector<int> p;
int fitness;
Individual(vector<int> p);
Individual mate();
int calc_fitness();
bool operator < (const Individual& tmp)const {
return fitness < tmp.fitness;
}
};
Individual::Individual(vector<int> P) {
this -> p = P;
this -> fitness = calc_fitness();
}
Individual Individual::mate() {
vector<int> _p = this -> p;
int P = random(0, 3);
for (int i = 1; i <= P; i ++ ) {
int pos1 = random(0, n - 1), pos2 = random(0, n - 1);
swap(_p[pos1], _p[pos2]);
}
return _p;
}
int Individual::calc_fitness() {
int state = 0;
for (int i = 0; i < n; i ++ ) {
for (int j = 0; j < K; j ++ )
state |= (1 << a[p[i]][j] - 1);
if (state == (1 << m) - 1) return i + 1;
}
puts("-1"); exit(0);
}
int main() {
scanf("%d%d%d", &n, &m, &K);
for (int i = 0; i < n; i ++ )
for (int j = 0; j < K; j ++ )
scanf("%d", &a[i][j]);
vector<Individual> population; vector<int> P;
for (int i = 0; i < n; i ++ ) P.push_back(i);
for (int i = 1; i <= POPULATION; i ++ ) {
random_shuffle(P.begin(), P.end());
population.emplace_back(Individual(P));
}
for (int i = 0; i < TIMES; i ++ ) {
sort(population.begin(), population.end());
ans = min(ans, population[0].fitness);
vector<Individual> new_population;
int s = (10 * POPULATION) / 100;
for (int i = 0; i < s; i ++ )
new_population.emplace_back(population[i]);
s = POPULATION - s;
for (int i = 0; i < s; i ++ ) {
Individual p = population[random(0, 50)];
new_population.emplace_back(p.mate());
}
population = new_population;
}
printf("%d\n", ans);
return 0;
}
例题三
对于这道题来说,最重要的是设计一个适应度函数。显然地,我们可以将适应度函数设计为当前点到 $n$ 个点的距离和。这样,适应度越小就越优秀。
在这道题里,染色体要设置成当前点的横纵坐标,这样怎么交配和变异呢?
首先先谈变异:我们可以将这个数写成二进制位,然后随机挑选一位取反。
对于交叉,我们可以使用原来的方法,也可以对于这个算法进行改进:为了避免答案精度过低,我们可以将父母双亲交配改成父代自交(也就是复制自己,随机变异几个点)产生后代。当然,我们会调高变异率。
代码如下,我加了部分注释:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <ctime>
#define x first
#define y second
#define TIMES 9
#define POPULATION 300
#define LEN 20
using namespace std;
const int N = 110;
int n, T;
pair<double, double> a[N]; // 存储 n 个点
int random(int l, int r) { // 产生从 l 到 r 之间的随机整数
return rand() % (r - l + 1) + l;
}
double dist(double x1, double y1, double x2, double y2) {
double dx = x1 - x2;
double dy = y1 - y2;
return sqrt(dx * dx + dy * dy);
}
// 下面正式进入遗传算法
struct Individual { // 存储个体信息的结构体
int x, y; // 个体的横纵坐标
double fitness; // 适应度
Individual(int x, int y);
Individual mate(); // 交配
double calc_fitness(); // 计算适应度
bool operator < (const Individual& tmp)const {
return fitness < tmp.fitness;
}
};
Individual::Individual(int x, int y) {
this -> x = x, this -> y = y;
this -> fitness = calc_fitness();
}
Individual Individual::mate() {
int chx = x, chy = y;
int p1 = random(0, 3); // 将 x 随机变异三个二进制位
for (int i = 1; i <= p1; i ++ ) {
int p = random(0, LEN);
if ((chx >> p) & 1) chx -= (1 << p);
else chx += (1 << p);
}
int p2 = random(0, 3);
for (int i = 1; i <= p2; i ++ ) {
int p = random(0, LEN);
if ((chy >> p) & 1) chy -= (1 << p);
else chy += (1 << p);
}
return Individual(chx, chy);
}
double Individual::calc_fitness() {
double ans = 0;
for (int i = 1; i <= n; i ++ )
ans += dist(a[i].x, a[i].y, (double)x / 100, (double)y / 100);
return ans;
}
int main() {
scanf("%d", &T);
while (T -- ) {
scanf("%d", &n);
for (int i = 1; i <= n; i ++ )
scanf("%lf%lf", &a[i].x, &a[i].y);
vector<Individual> population;
for (int i = 0; i < POPULATION; i ++ ) {
int x = random(0, 1000000);
int y = random(0, 1000000);
population.push_back(Individual(x, y));
}
for (int i = TIMES; i >= 1; i -- ) { // 这里的 i 被当做了 t
sort(population.begin(), population.end());
vector<Individual> new_population;
int s = (10 * POPULATION) / 100;
for (int i = 0; i < s; i ++ ) // 保留精英种子
new_population.push_back(population[i]);
s = POPULATION - s;
while (new_population.size() < POPULATION) {
int len = population.size();
Individual p = population[random(0, 50)];
Individual q = p.mate();
double delta = q.fitness - p.fitness;
if (delta < 0) new_population.emplace_back(q);
else if ((double)exp(-delta / i) / 2.0 > (double)rand() / RAND_MAX)
new_population.emplace_back(q); // 概率接受
}
population = new_population;
}
printf("%.0lf", population[0].fitness); if (T) putchar('\n');
getchar();
}
return 0;
}
- Q:为什么这里要存储二十位二进制呢?
- A:由于坐标范围在 $0$ 到 $10 ^ 4$ 之间,而且我们要精确到两位小数。因此要将两位小数变成整数存储。这样,我们就要存储 $[0, 10 ^ 6]$ 之间的整数。将这个整数除以 $100$ 就可以解码变为原来的坐标。由于 $\log _2 10^6$ 大约等于 $20$,我们就将二进制位的长度设成这个长度。
其他例题
基本上模拟退火能做的遗传都能搞。
物竞天择,适者生存。这是每个世界都适用的生存法则。
本文参考资料 Genetic Algorithms。
后记
1.关于遗传算法和模拟退火算法的比较
遗传算法的缺点就是收敛慢。对于求解最短哈密尔顿回路问题,遗传算法和模拟退火算法的表现如下(数据中 $n = 70$):
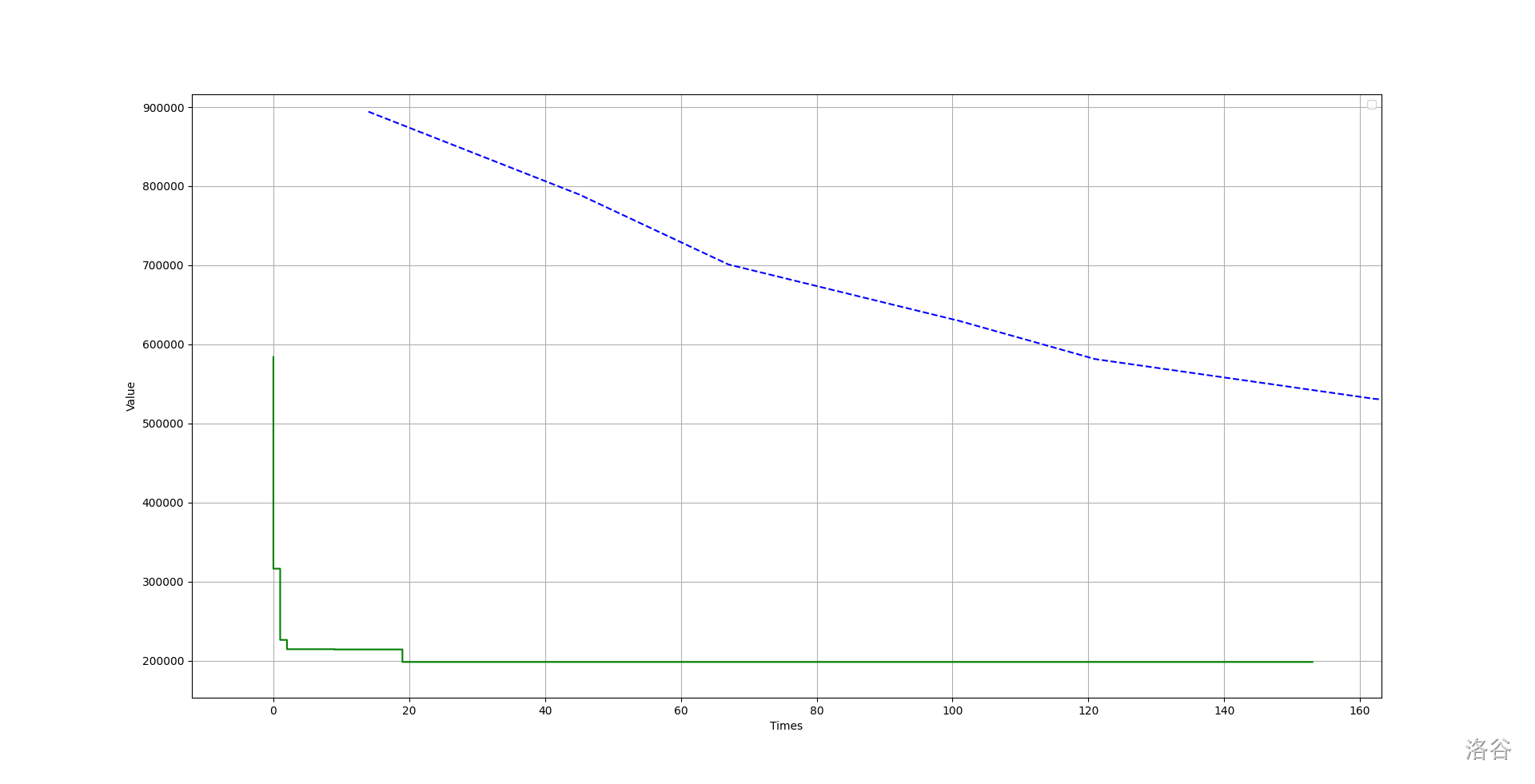
其中蓝色虚线是遗传算法,绿色实线是模拟退火算法。
可以看出,模拟退火算法收敛的很快,而遗传算法表现略逊。
实际上,在大部分问题上模拟退火表现都比遗传算法优秀得多。
但是遗传算法在某些问题上还是有实践意义。对于某些数据量较大的情况,遗传算法更具有优势。还是拿刚才的求解哈密尔顿回路的问题举例。对于同一组数据,虽然模拟退火收敛较快而且在短时间内效果极好,但是在后期明显不如遗传算法。
2.对于 Stoffa 改进方法的概率接受
还是拿收敛到最低适应度举例。假设后代适应度为 $y$,父代适应度为 $x$,有 $\Delta = y - x$。若 $\Delta < 0$,证明子代比父代更好,我们一定接受。对于 $\Delta > 0$,证明子代不如父代好,我们以一定概率接受。上文给出了概率计算函数:
$$P(\Delta) = e ^ { - \Delta / t}$$
其中 $t$ 是我们设定的参数值,一般随着迭代次数增大而减小。如果 $P(\Delta) > \operatorname{rand}(0, 1)$,那么我们就接受它。
但是如果我们考虑一个极端情况:不妨先假设 $t$ 此时等于 $1$,那么$P(\Delta) = e ^{- \Delta}$。在假设 $\Delta > 0$ 且足够小(趋于 $0$),那么我们接受这个解的概率就非常大。然而在我们的直觉中,这个概率应该小于 $50 \%$ 而且趋于 $50 \%$。因此这就是遗传算法的另一个改进方法,即将概率计算函数改为:
$$P(\Delta) = \dfrac{1}{2} e ^ {- \Delta / t}$$
其中这个 $\dfrac{1}{2}$ 可以自主调节的。目的就是使得较劣解不会被接受。
这种方法在模拟退火上同样可以应用,实测具有较好的优化效果。在其他网站上针对题目 UVA10228 A Star not a Tree? 进行测试,未进行优化需要跑 $12$ 遍退火,然而优化后只需要跑 $2$ 次。
下面是对于求解 $n = 18$ 的哈密尔顿路径时的优化效果:
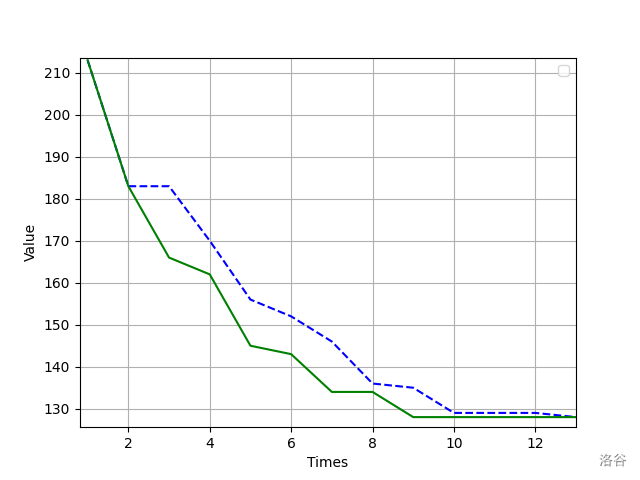
其中蓝色虚线使用的是没有改进的接受函数,而绿线使用的是改进后的接受函数。可以看出,的确存在一定的优化效果。


ojrz
佬!
ojrz
冒昧地问一句,$ojrz$ 是什么意思?
大佬磕一个😂
象形的符号