分组背包问题

相较于之前的背包问题
在分组背包问题中，给定若干组物品
每组物品有若干个，每组物品中每件物品的体积和价值不一定相同
但同样一组物品中最多只能选一个物品

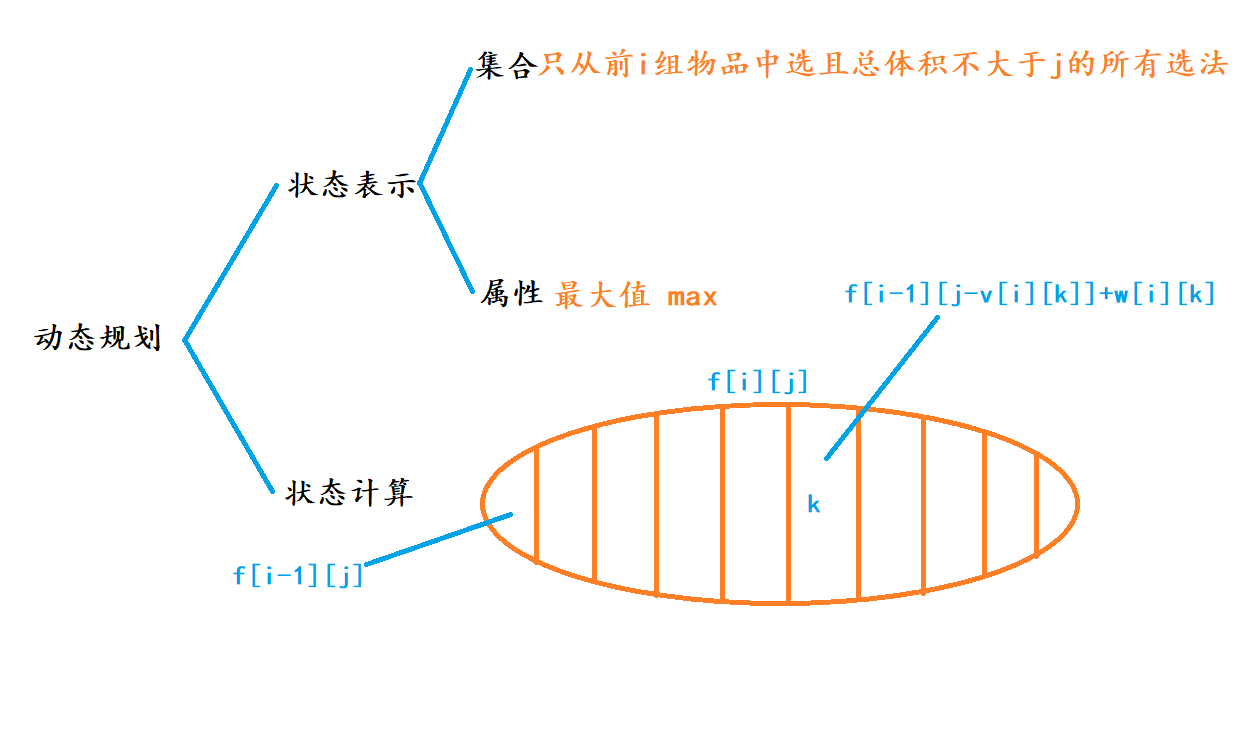
状态表示 $f[i][j]$ (化整为零)
$f[i][j]$表示集合的属性
通过一个数组来表示只从前$i$组物品中选择，且总体积不超过$j$时的最大价值

属性：背包中元素的最大价值（max）

状态计算——集合的划分（化零为整）

将集合划分为$k$个集合
类似地，对于集合$f[i][j]$我们将其同样划分为：

• 不包含第$i$组物品（从前$i-1$组物品中选）
• 包含一个第$i$组物品
• 包含两个第$i$组物品
• ......
• 包含$k$个第$i$组物品 $(k\leq s[i])$

当我们不包含该组物品时，此时的状态应该是$f[i-1][j]$

当我们包含该组物品时，我们从$[1,s[i]]$依次枚举该组物品并更新状态使得总价值最大
此时的状态为$f[i-1][j-v[i][k]]+w[i][k]$

状态转移方程：

$\color{red}{f[i][j]=max(f[i-1][j],f[i][j]-v[i][k]+w[i][k])}$

C++代码

#include<bits/stdc++.h>

using namespace std;

const int N = 110; //数据范围100

int n, m; //输入的n.m值表示物品组数和背包容量
int v[N][N], w[N][N], s[N]; //v表示体积 w表示价值 s表示某组物品中的物品数量
int f[N]; //状态表示

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ )
    {
        cin >> s[i]; //存入某组物品的数量
        for (int j = 0; j < s[i]; j ++ )
            cin >> v[i][j] >> w[i][j]; //存入该组物品某个物品的体积和价值
    }

    for (int i = 1; i <= n; i ++ )
        for (int j = m; j >= 0; j -- )
            for (int k = 0; k < s[i]; k ++ )
                if (v[i][k] <= j)
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);

    cout << f[m] << endl;

    return 0;
}