题目描述

给定N个闭区间$[ai,bi]$，请你在数轴上选择尽量少的点，使得每个区间内至少包含一个选出的点。

输出选择的点的最小数量。

位于区间端点上的点也算作区间内。

输入格式

第一行包含整数N，表示区间数。

接下来N行，每行包含两个整数$ai,bi$，表示一个区间的两个端点。

输出格式

输出一个整数，表示所需的点的最小数量。

数据范围

$1≤N≤1e5$,
$−1e9≤ ai ≤ bi ≤ 1e9$

样例

输入样例：

3
-1 1
2 4
3 5

输出样例：

2

思路
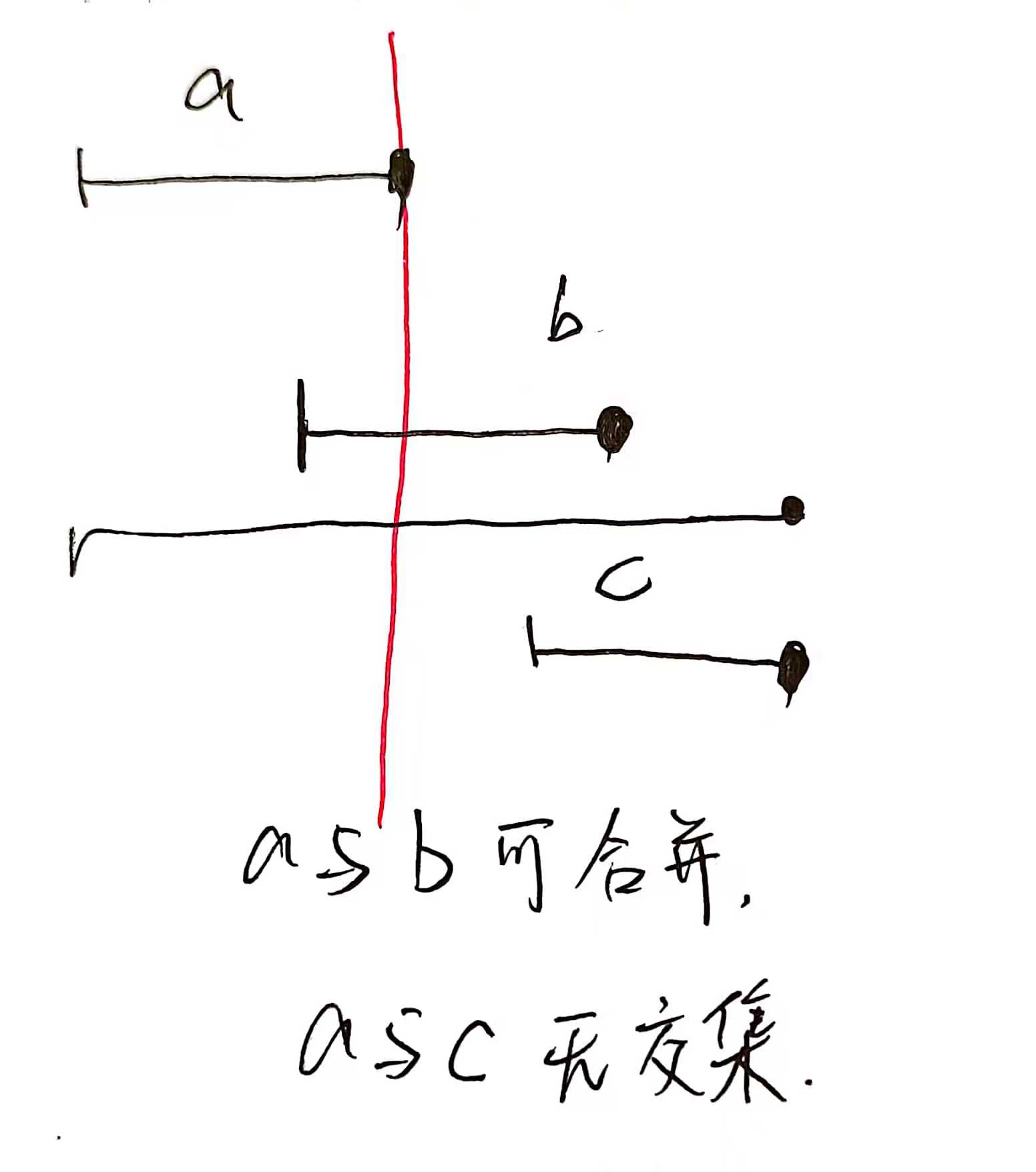
就是求有多少个不能有交集的区间，有交集的可以合并。按所有区间右端点从小到大排，遍历所有区间，设要比较的是a 区间的右端点，若有区间左端点小于a的右端点，即区间可以合并；若有区间左端点大于a 的右端点，没有交集，即二者没有交集，res++，更新要枚举的右端点.

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 1e5+10;

struct Range
{
    int l, r;

    bool operator < (const Range& t) //按区间右端点从小到大排序
    {
        return r < t.r; 
    }
}range[N];

int n;

int main()
{
    cin >> n;
    for (int i = 0; i < n; i++) cin >> range[i].l >> range[i].r;
    sort(range, range+n);

    int res = 0; //一共有多少个没有交集
    int right = -2e9; //上一个区间的右端点，初始化为最小的数
    for (int i = 0; i < n; i++) //枚举区间
    {
        if (range[i].l > right) //若当前区间左端点大于上一区间右端点，说明没有交集
        {
            res++;
            right = range[i].r;
        }
    }

    cout << res;

    return 0;
}