C++

$\color{gold}{— > 蓝桥杯辅导课题解}$

思路：

贪心 进位制

X 进制：

平时我们所说的10进制数是怎么得出来的呢？
比如10进制数 123: 它是由百位上的1 * 10 * 10 加上 十位上的 2 * 10 加上 个位上的 3 得出来的


关于x进制转10进制：
比如题目中给的：11进制（10）、5进制（4）、2进制（0）
                对于i位上的数字num[i]，转换为十进制就是num[i]*低于i位所有位的进制
                就是10*5*2+4*2+0=108
        再比如：11进制（1）、5进制（2）、2进制（0）        
                就是1*5*2+2*2+0=14


题目要求： X 进制下 A - B 的最小值  

只需 A B 对应数位上的数字取得其合法的最小进位制即可

$\color{red}{图解：}$

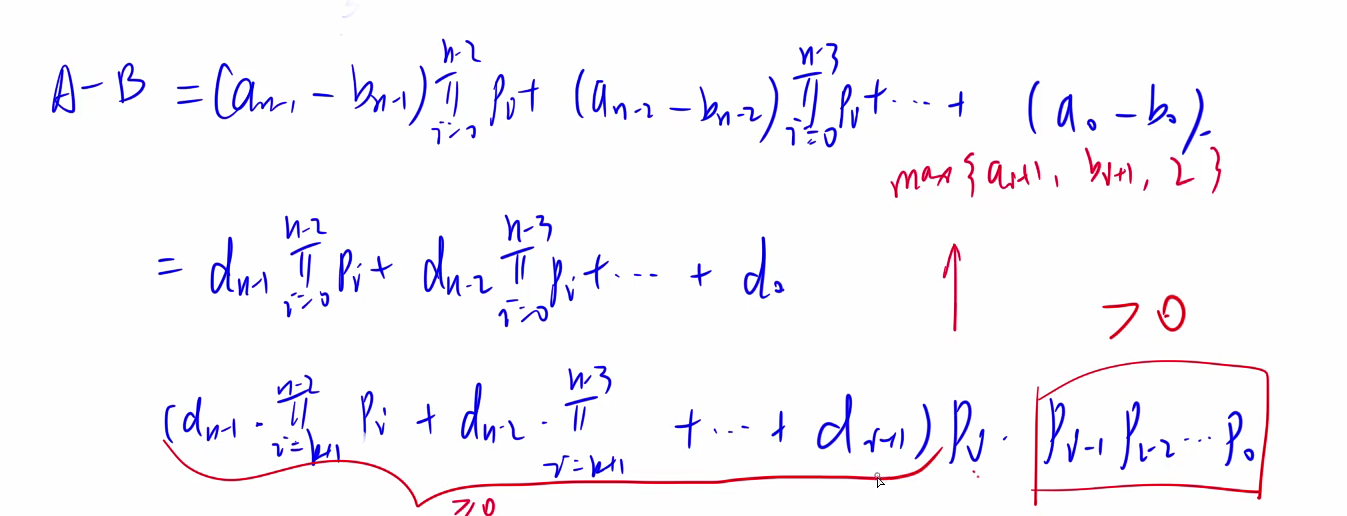
#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10, MOD = 1000000007;
typedef long long ll;

int n, m1, m2, m;
int a[N], b[N];

int main() {
    cin >> n;
    cin >> m1;
    for (int i = m1 - 1; i >= 0; i --) cin >> a[i]; // 逆序存储，a[0]存储个位，a[1]存储十位
    cin >> m2;
    for (int i = m2 - 1; i >= 0; i --) cin >> b[i];

    int m = max(m1, m2);

    int res = 0;
    for (int i = m - 1; i >= 0; i --) 
        res = (res * (ll)max({2, a[i] + 1, b[i] + 1}) + a[i] - b[i]) % MOD;

    cout << (res + MOD) % MOD;    
    return 0;
}