莫比乌斯函数：

题意：给定a,b,d，若$1≤x≤a，1≤y≤b$，求有多少对x和y,使得$(x,y)=d$。

转化=>令$x’=x/d，y’=y/d$，则$1≤x’≤a/d，1≤y’≤b/d$，求有多少对x'和y'互质,。

如何求总共有多少对合法的呢？这里用到补集的思想：合法对数= 总对数-不合法对数。

不合法对：x'和y'的最大公因数大于1。
令$a’=a/d，b’=b/d$，利用容斥原理求得不合法对数：

$a’b’-a’/2 * b‘2-a’/3 * b’/3 - …(有一个质公因子)$

$\ \ \ \ \ \ $$+a’/6 * b’/6 + …\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (有两个不同质公因子)$

$\ \ \ \ \ \ $$-a’/30 * b’/30 - …\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (有三个不同质公因子)$

=>$\sum_{i=1}^{min(a’,b’)}a’/i * b’/i * mobius[i]$
发现如果要这样做i就要枚举$1-N$，因此每次的时间复杂度是$O(n)$的,有$N=50000$，会$TLE$，所以还要优化。

如何优化？

发现，这个式子中虽然i要枚举$N$次，但是实际上因为整除的原因$\frac{a}{i}$的值很少，只有$2\sqrt{a}$个！
因为$\frac{a}{1}$、$\frac{a}{2}$、$\frac{a}{3}$、…是单调递减的，所以整个序列的值可以分成$2\sqrt{a}$段相同的值。

说明：1、为什么是$2\sqrt{a}$段 2、怎么分

1、
将原来的n项分为两部分：
$\ \ \ \ \ 1、\frac{a}{1} - \frac{a}{\sqrt{a}}$ 有$\sqrt{a}$项
$\ \ \ \ \ 2、\frac{a}{\sqrt{a}+1} - \frac{a}{a}$ 有$\sqrt{a}$个取值

2、
设g(x)表示使$\frac{a}{x}$的取值不变的最大的x值，就有$\frac{a}{x}$=$\frac{a}{g(x)}$，且$\frac{a}{x}$>$\frac{a}{g(x)+1}$，其中$g(x) = \frac{a}{\frac{a}{x}}$
证：$\frac{a}{x}$=$\frac{a}{g(x)}$

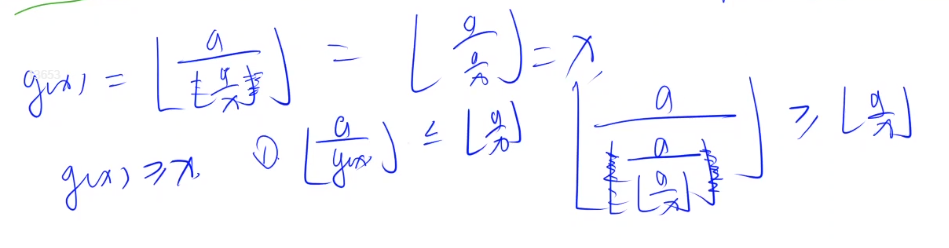
只有这一条式子无法保证时间复杂度，因为虽然知道从$x$跳到$g(x)$，分式的值不变，但是不知道$g(x)$是不是$x$所能达到的最大值，因此需要证下式!

证：$\frac{a}{x}$>$\frac{a}{g(x)+1}$

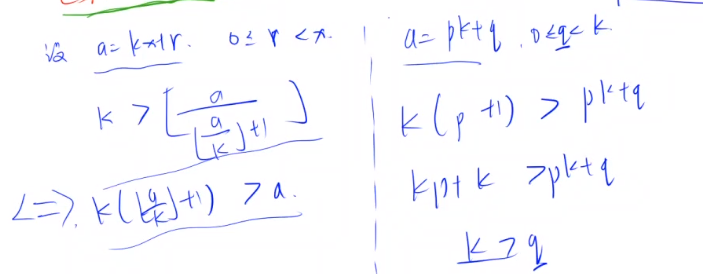
由这条式子可以得知，$g(x)$可以使分式的值不变，但是$g(x)+1$却小于，说明$g(x)$是$x$所能达到的最大值！
综上：将原来的序列分成$2\sqrt{a}$段，而且每次都会跳一段，所以总共会跳$2\sqrt{a}$次，时间复杂度就是$O(\sqrt{a})$!

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 50010;

int primes[N] , cnt;
bool st[N];
int mobius[N] , sum[N];

void init(int n)
{
    mobius[1] = 1;
    for(int i = 2 ; i <= n ; i++)
    {
        if(!st[i]) 
        {
            primes[cnt++] = i;
            mobius[i] = -1;
        }

        for(int j = 0 ; primes[j] <= n / i ; j++)
        {
            int t = primes[j] * i;
            st[t] = true;
            if(i % primes[j] == 0)
            {
                mobius[t] = 0;//t中至少包含2个primes[j]
                break;
            }
            mobius[t] = mobius[i] * -1;//primes[j]只出现一次，所以t的mobius值取决于i
        }
    }

    for(int i = 1 ; i <= n ; i++) sum[i] = sum[i - 1] + mobius[i];
}

int main()
{
    init(N - 1);

    int T;
    cin >> T;
    while(T--)
    {
        int a , b , d;
        cin >> a >> b >> d;
        a /= d , b /= d;
        int n = min(a , b);
        LL res = 0;
        for(int l = 1 , r ; l <= n ; l = r + 1)
        {
            r = min(n , min(a / (a / l) , b / (b / l)));
            //x最远跳到的位置g(x) = t / (t / x)，因为要使a/l和b/l的值都不变，所以要取跳的位置的min
            res += (sum[r] - sum[l - 1]) * (LL)(a / l) * (b / l);
            //在x∈[l,r]上，a/x和b/x的值是不变的，所以只要求出l~r上mobius的和*分式的值即可
        }
        cout << res << endl;
    }
    return 0;
}