$\color{green}{<–画图不易，点下这里赞一下吧}$

我们的目的是，找到一种选择方案，在背包能装下的情况下，使得选择物品的总价值最大，然后输出总价值。

动态规划解题步骤

动态规划问题，一般从三个步骤进行考虑。

步骤一：集合及集合的状态。

所谓的集合，就是一些方案的集合。

用 g[i][j] 表示从前 i 种物品中进行选择，且总体积不大于 j 的各个选法获得的价值的集合。注意，g[i][j] 是个集合，表示一堆数：所有可能选出的价值。

例如 g[2][3] 从前 2 种物品中进行选择，且总体积不大于 3 的各个选法获得的价值的集合。选择方案有三种：都不选，价值为 0、选择第 1 个物品，价值为 2、选择第 2 个物品，价值为 4、选择第 1，第 2 个物品，价值为 6。 g[2][3] = {0, 2, 4, 6}。

例如 g[3][4] 从前 3 种物品中进行选择，且总体积不大于 4 的各个选法获得的价值的集合，选择方案有三种：都不选，价值为 0、选择第 1 个物品，价值为 2、选择第 2 个物品，价值为 4、选择第 3 个物品，价值为 4，选择第 1，第 2 个物品，价值为 6，选择第 1，第 3 个物品，价值为 6。 g[3][4] = {0, 2, 4, 4, 6, 6}。

i j 取不同的值，对应不同的 g[i][j]，也就是对应不同的集合。

用 f[i][j] 表示从前 i 种物品中进行选择，总体积小于等于 j 所能获得的最大价值, 注意，f[i][j] 是个一个数，是g[i][j] 这个集合中的最大值。很明显，f[i][j] 就是 g[i][j] 中的最大值。i j 取不同的值，就对应不同的 f[i][j]，即对应不同的集合的最大值。

例如 f[2][3] 表示从前 2 种物品中进行选择，且总体积不大于 3 的获得的最大价值。f[2][3] = max(g[2][3]) = 6。

例如 f[3][4] 表示从前 3 种物品中进行选择，且总体积不大于 4 的获得的最大价值。f[3][4] = max(g[3][4]) = 6。

g[i][j] 的最大值就是 f[i][j]。

如果我们能把所有集合对应的最大值都求出来，即求出了 f[0][0] ~ f[N][V]， f[N][V] 的含义是在前 N 种物品中进行选择，总体积不大于 V 所获得的最大价值，就是我们要找的答案。

注意，我们不需要把各个集合的所有元素都找出来，只需要求出各个集合的最大值就能找到答案。下面就是如何求出各个集合的最大值。

步骤二：状态计算（求某个集合的最大值）。

g[i][j] 是从前 i 个物品中进行选择，且总体积不大于 j 的各个选法获得的价值的集合。

f[i][j] 是从前 i 种物品中进行选择，总体积小于等于 j 所能获得的最大价值。

f[i][j] 是集合 g[i][j] 的最大值。

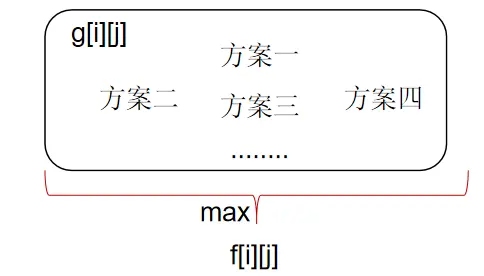
所谓的状态计算是指，如何将 f[i][j] 算出来。

如果把各个集合 g[i][j] 的状态 f[i][j] 求出来， f[N][V] 就是要找的答案。

对于上面的例题，g[2][3] 表示从前 2 种物品中选择，总体积小于等于 3 的所有选择方案获得的价值的集合。

选择方案有 三 种：方案1. 只选物品1，价值为 2。 方案2. 只选物品 2，价值为 4。方案3. 同时选物品 1 和物品 2，价值为 6。

g[i][j] = {2， 4， 6}。f[i][j] 为该集合中的最大值 6。

为了求出f[i][j]，我们可以使用下面的方法。

将 g[i][j] 这个集合划分成互斥的 A B 两部分。

A 部分是选法中不包含第 i 件物品。B 部分是选法中包含第 i 件物品。只要将 A 部分的最大值和 B 部分的最大值求出来，两者中较大的值就是 g[i][j] 的最大值，也就是 f[i][j]。。

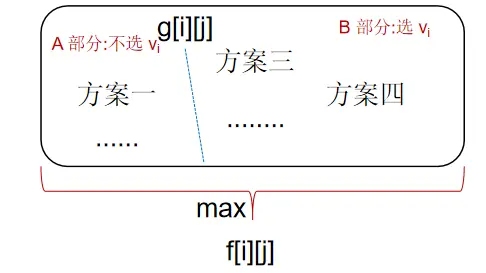
A 部分，等价于从前 i - 1 件物品中选择，选出的物品总体积小于等于 j 的所有方案获得的价值集合，也就是 g[i - 1][j]。g[i - 1][j]这个集合中的最大值是 f[i - 1][j]，所以 A 部分的最大值就是 f[i - 1][j]。

B 部分等价于从前 i 件物品中选择，并且必须选择第 i 件物品，且选出的物品总体积小于等于 j 的所有方案获得的价值集合。

B 部分怎么求呢？直接求不太好求，可以试试曲线救国：

因为 B 部分对应的方案中一定要选择第 i 件物品。这时候有两种情况。

• 给定的容量能放下第 i 件物品，那么第 i 件物品会占据 $v_i$ 的背包空间，剩下的背包空间为 j - $v_i$ 。可以继续从前 i - 1 种物品中，选出的物总体积小于等 j - $v_i$的物品放入背包中。

  从前 i - 1 种物品中进行选择，选出的物总体积小于等 j - $v_i $ 的方案获得的价值集合为 g[i - 1][j - $v_i$] 。所以 B 部分的元素为 g[i-1][j - $v_i$] 中各个元素的值加上 $w_i$ 。g[i-1][j - $v_i$] 中的最大值为 f[i-1][j - $v_i$]， 因此 B 部分的最大值为 f[i-1][j - $v_i$] + $w_i$ 。

• 给定的容量不能能放下第 i 件物品，这时候背包里就不能放入第 i 件物品，因此 B 部分就是空集。B 部分的最大值为 0。

例如 g[2][3] 可以划分成两部分，A 部分是不包含第 2 种物品，对应方案1。B部分是包含第 2 种物品，对应方案 2 和方案 3。

A 部分的最大值是 f[2 - 1][3] = f[1][3] = 2。

B 部分的最大值是 f[2 - 1][3 - 2] + $w_2$ = f[1][1] + 4 = 6。

所以集合g[2][3] 的最大值 f[2][3] = max(A，B) = max(2, 6) = 6。

通过上面分析，我们可以知道，g[i][j] 可以分成两部分，A 部分是不包含第 i 种物品对应所有选法获的价值的集合，最大值是 f[i - 1][j]。B 部分是包含第 i 种物品对应所有选法获的价值的集合，最大值是 f[i-1][j - $v_i$] + $w_i$ 或 0。所以 g[i][j] 的最大值就是在 A 部分的最大值与 B 部分的最大值取个max，也就是:

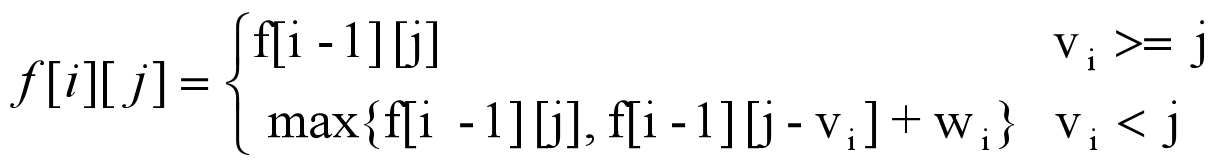
从计算公式可以看出，f[i][j] 是由 f[i - 1][j -$ v_i$ ] 和 $w_i$ 计算出来的。也就是f[i][j]的值是可以从前面已经计算出的 f 值求出来。如果我们能确定 f[i][j] 的一部分初始值，就能通过该公式，一步步计算得出 f[N][V]，也就是我们要找的答案。

步骤三：确定初始值

0 1 背包问题的有些状态是能够直接确定的。

例如 f[0][0]。

f[0][0] 的含义是从前 0 件物品中选择，并且选出的物品总体积小于等于0 时所能得到的最大价值。总体积小于等于 0，说明一种物品都不能选择，因此 f[0][0] = 0。同理 f[1][0] = 0，f[2][0] = 0 ··· f[N][0] = 0。

有了这些初始值，通过 i 从 1 遍历 N，j 从 1 遍历 V，就能一步步求出所有的 f[i][j] 了。

例如求 f[1][1]。f[1][1] = max(A, B) = max{f[0][1]，f[0][0] + 2} = max(0，2) = 2。

求 f[1][2]。f[1][2] = max(A, B) = max{f[0][2]，f[0][0] + 2} = max(0，2) = 2。

最后 f[N][V] 就是要找的答案。

这时候就可以写代码了：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];//v 保存体积，w 保存价值
int f[N][N];//保存所有集合最值状态

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ )
        cin >> v[i] >> w[i];

    for(int i = 0; i <= m; i++)//初始化，前 0 中物品中选择
    {
        f[0][i] = 0;
    }

    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++)
        {
            if(v[i] <= j)//能放入第 i 件物品的情况下，求f[i][j]
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
            else//不能放入第 i 件物品的情况下，求f[i][j]
                f[i][j] = f[i - 1][j];
        }

    }
    cout << f[n][m] << endl;//f[n][m] 就是答案

    return 0;
}

优化

动态规划的优化一般都是对代码或者集合最值方程进行一个等价变形。在考虑动态规划问题的时候，一定要先把基本的形式写出来，然后再对它进行优化。

首先，根据优化前的起码，f[i][j] 是从上到下，一行一行这样填满的：

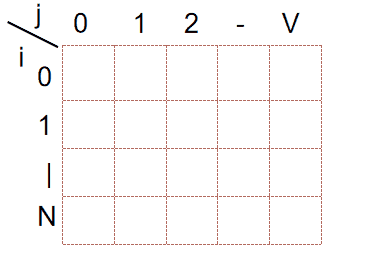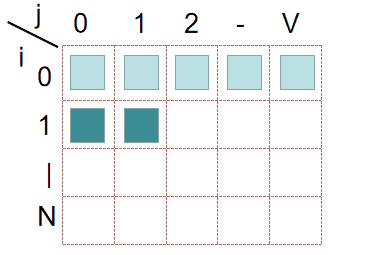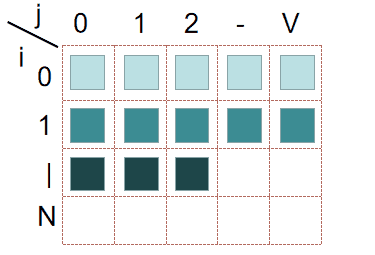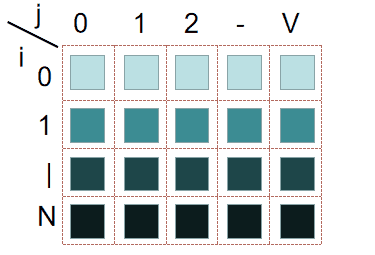
看一下 f[i][j] 的计算公式：f[i][j] = max(A, B)。

只用到了f[i - 1][j]，f[i-1][j - $v_i$] ，即只用到了 f[i - 1] 这一层，并且用到的体积为 j 和 j - $v_i$ ，都是小于等于 j 的。

因此可以从体积为 V 开始，利用f[i - 1]的数据，求解出 f[i][j]，把 f[i][j] 放到 f[i -1][j] 的位置上。这样 f 数组就能优化到一维了。

并且，当 背包容量小于 $v_j$ 的时候，f[i][j] = max{f[i - 1][j]，0} = f[i - 1][j]。所以 j 只需要从 V 遍历到 $v_j$ 即可。

写下代码：

//参考yxc
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = m; j >= v[i]; j -- )
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;

    return 0;
}

0 1背包问题到此解决。