最近公共祖先【模板题】，爬山法 $O(n)$

题目理解：

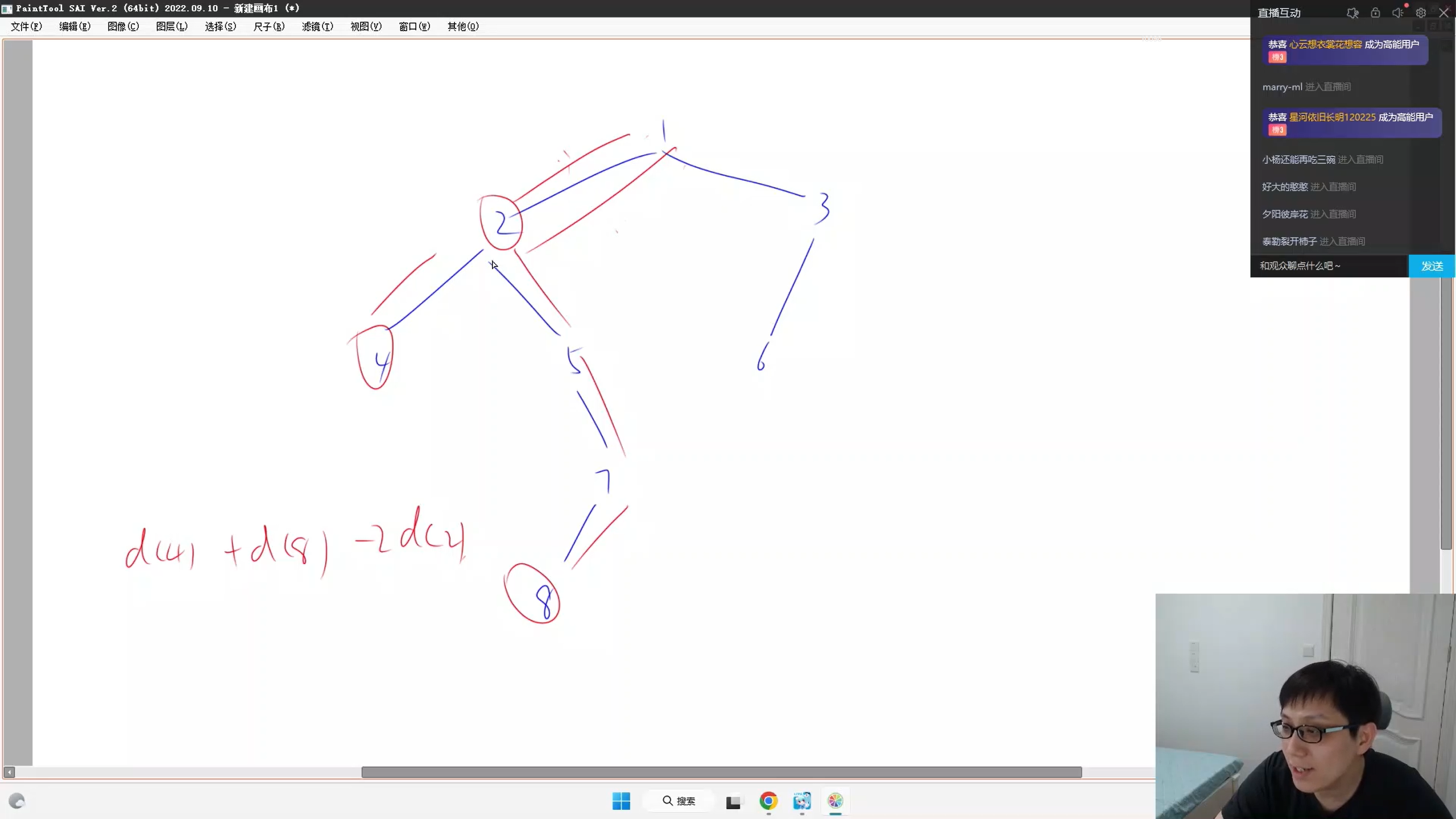
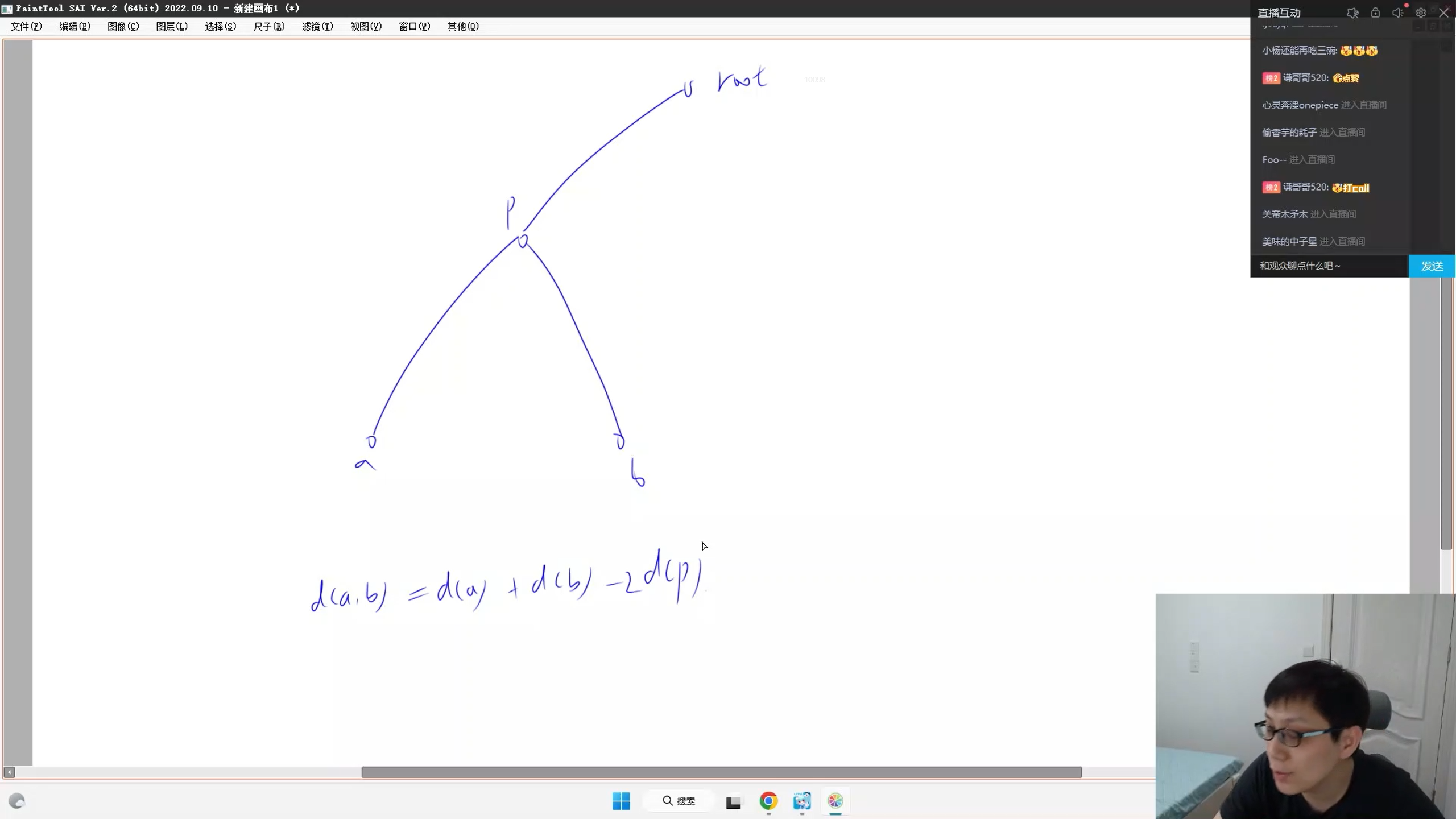
手玩样例，可以发现 ： d(a, b) = d[a] + d[b] - 2 * d[p], 其中，d[] 表示 到根节点的距离， p表示 (a, b)的最近公共祖先

即 难点为： 如何求 最近公共祖先 ？

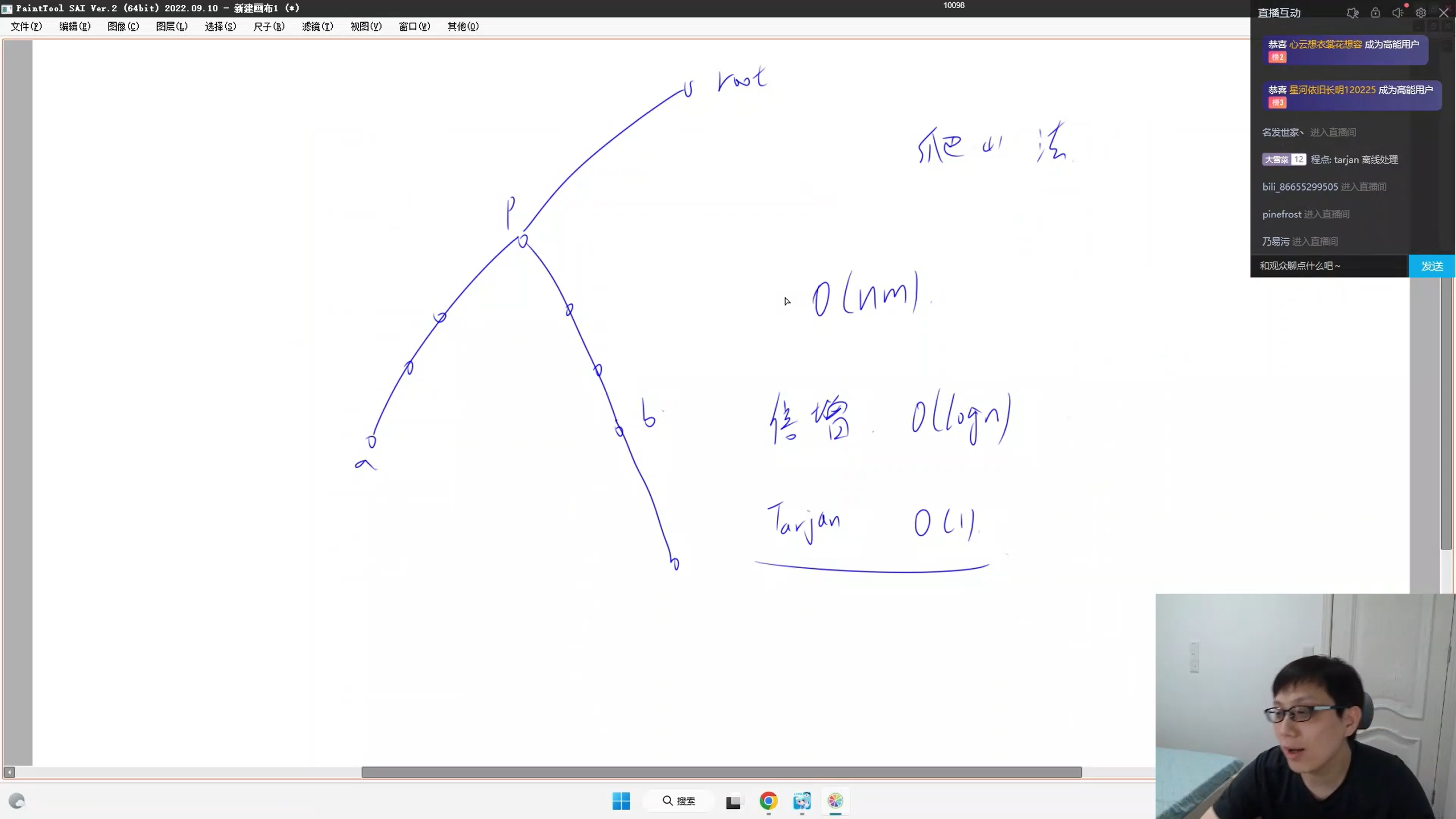
有3种算法：

1. 爬山法 O(n)
2. 倍增 O(logn) 【未学】
3. Tarjan O(1) 【未学】

结合题目数据范围， 爬山法即可， 总 时间复杂度 $ O(n * m) $

本题 收获：

1. 建树，左右儿子，父节点
2. dfs 求 距离
3. 爬山法O(n) 求 最近公共祖先

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int l[N], r[N], p[N];
int dist[N];

void dfs(int u, int d)
{
    dist[u] = d;
    if(l[u] != -1) dfs(l[u], d + 1);
    if(r[u] != -1) dfs(r[u], d + 1);
}

int get_lca(int a, int b) // 爬山法 求最近公共祖先，O(n)
{
    if(dist[a] > dist[b]) swap(a, b); // 默认 d[b] 大

    while(dist[b] > dist[a]) b = p[b];
    while(a != b) a = p[a], b = p[b];
    return a;
}

int main()
{
    int T;
    scanf("%d", &T);

    while( T -- )
    {
        scanf("%d%d", &n, &m);
        for (int i = 1; i <= n; i ++ )
        {
            int a, b;
            scanf("%d%d", &a, &b);

            l[i] = a, r[i] = b;
            if(a != -1) p[a] = i;
            if(b != -1) p[b] = i;
        }

        dfs(1 ,0);

        while (m -- )
        {
            int a, b;
            scanf("%d%d", &a, &b);

            int lca = get_lca(a, b); // 爬山法 O(n)

            printf("%d\n", dist[a] + dist[b] - dist[lca] * 2);
        }
    }

    return 0;
}