3305. 作物杂交

思路

闫式 $DP$ 分析法：

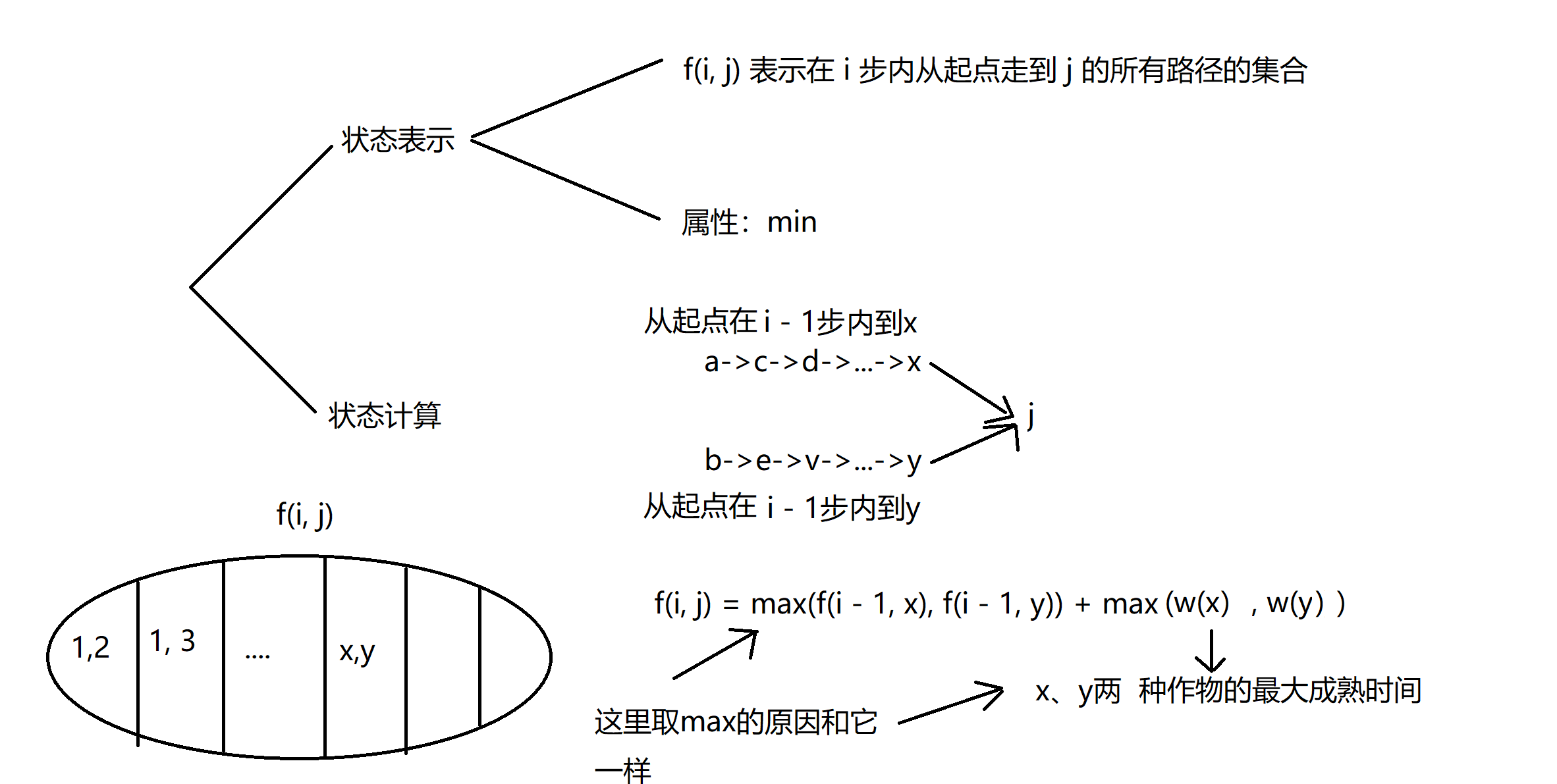
当然如果是朴素地按照图中的状态转移方程，一共有 $n - 1$ 步，每一步最坏情况下需要从 $k$ 条边取一个 $max$，时间复杂度 $O(nk)$，会 $TLE$（即 $bellman-ford$ 算法的做法）。

如果用 $spfa$ 算法，那么我们只需要在 $x$ 被更新（就是在队列中的点，因为队列中存储的就是被更新距离的点）的时候，再取出能够和 $x$ 杂交的所有 $y$，然后更新 $x * y->z$ 这些边对应的终点 $z$ 的距离即可，时间复杂度优于 $O(nk)$（不过最坏情况也是 $O(nk)$）

当然代码实现上，我们仅仅使用一维数组 $f$ 存储所有距离即可。

如果担心 $spfa$ 被卡的话，因为边权都是正数，所以本题可以使用 $dijkstra$，朴素版 $O(n^2)$，堆优化版 $O(mlogn)$，在本题中都能过。这里给出堆优化版的代码。

spfa代码

#include <iostream>
#include <queue>
#define endl "\n"
using namespace std;

const int N = 2010, M = 200010;
const int INF = 0x3f3f3f3f;

int n, m, k, ed;
int e[M], ne[M], t[N], to[M], idx;
int f[N], h[N];
bool st[N];
queue<int> q;

void add(int x, int y, int z)
{
    e[idx] = y, ne[idx] = h[x], to[idx] = z, h[x] = idx++;
}

void spfa()
{
    while(q.size())
    {
        int x = q.front();
        q.pop();
        st[x] = false;

        for(int i = h[x]; i != -1; i = ne[i])
        {
            int y = e[i], z = to[i];
            if(f[z] > max(f[x], f[y]) + max(t[x], t[y]))
            {
                f[z] = max(f[x], f[y]) + max(t[x], t[y]);
                if(!st[z]) q.push(z), st[z] = true;
            }
        }
    }
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> n >> m >> k >> ed;
    for(int i = 1; i <= n; i++) h[i] = -1, f[i] = INF;
    for(int i = 1; i <= n; i++) cin >> t[i];
    while(m--)
    {
        int x;
        cin >> x;
        f[x] = 0;
        q.push(x);
    }
    while(k--)
    {
        int x, y, z;
        cin >> x >> y >> z;
        add(x, y, z), add(y, x, z);
    }

    spfa();

    cout << f[ed] << endl;
    return 0;
}

堆优化版dijkstra

#include <iostream>
#include <queue>
#define x first
#define y second
#define endl "\n"
using namespace std;

const int N = 2010, M = 200010;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> PII;

int n, m, k, ed;
int e[M], ne[M], t[N], to[M], idx;
int h[N], f[N];
bool st[N];
priority_queue<PII, vector<PII>, greater<PII>> q;

void add(int x, int y, int z)
{
    e[idx] = y, ne[idx] = h[x], to[idx] = z, h[x] = idx++;
}

void dijkstra()
{
    while(q.size())
    {
        PII cur = q.top();
        q.pop();

        int x = cur.y;
        if(st[x]) continue;
        st[x] = true;

        for(int i = h[x]; i != -1; i = ne[i])
        {
            int y = e[i], z = to[i];
            if(f[z] > max(f[x], f[y]) + max(t[x], t[y]))
            {
                f[z] = max(f[x], f[y]) + max(t[x], t[y]);
                q.push({f[z], z});
            }
        }
    }
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> n >> m >> k >> ed;
    for(int i = 1; i <= n; i++) h[i] = -1, f[i] = INF;
    for(int i = 1; i <= n; i++) cin >> t[i];
    while(m--)
    {
        int x;
        cin >> x;
        f[x] = 0;
        q.push({f[x], x});
    }
    while(k--)
    {
        int x, y, z;
        cin >> x >> y >> z;
        add(x, y, z), add(y, x, z);
    }

    dijkstra();

    cout << f[ed] << endl;
    return 0;
}