遍历数组，然后再遍历每一个窗口

时间复杂度 $ O(nk) $

优化

通过单调性优化。

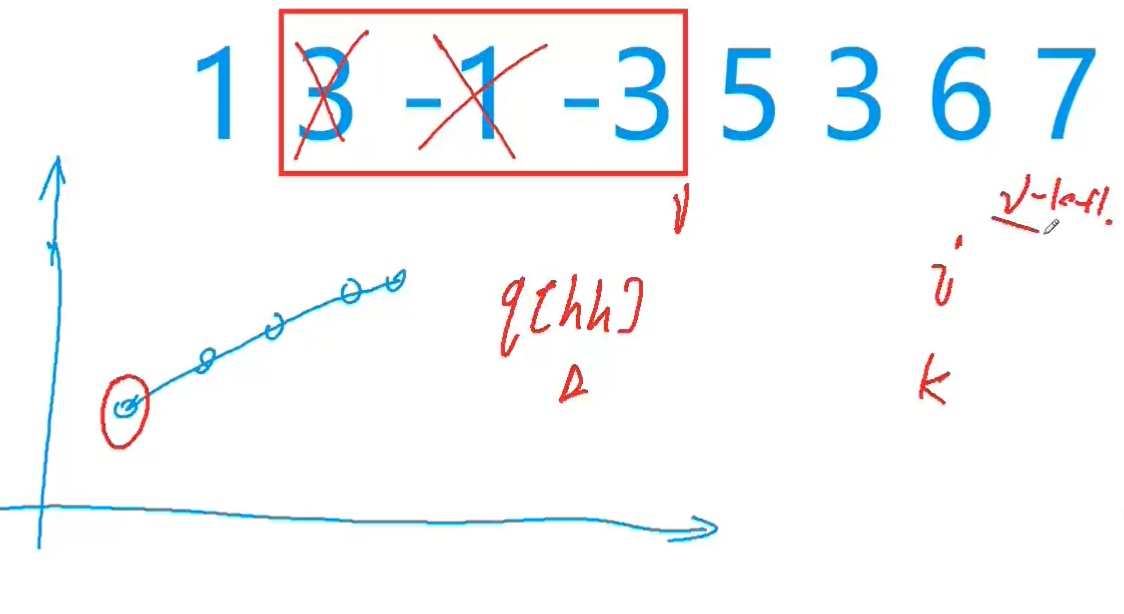
我们观察一个规律，对于3 -1 -3， 当-3存在， 并且寻找滑动窗口内的最小值时，3 -1是无效的， 也就是说，当-3加入队列时，-1删去， 3也删去。

抽象一些，当入队元素小于等于队尾元素， 队尾元素出队。直到入队元素大于队尾元素a[q[tt]] >= a[i]， 或者队列为空，则停止删除操作。

while (hh <= tt && a[q[tt]] >= a[i]) tt -- ;

k表示滑动窗口大小， q[N] 存储的是数组下标

需要保证q数组里面存储的元素小于等于k

if (hh <= tt && i - k + 1 > q[hh]) hh ++ ;

当滑动窗口里面的元素个数等于k个的时候才能输出

当k=3， 滑动窗口需要有三个元素才能开始输出最值

if (i >= k - 1) printf("%d ", a[q[hh]]);

#include<iostream>
using namespace std;
const int N=1e6+10;
int q[N], a[N];

int main(){
    int n, k;
    cin>>n>>k;
    for(int i=0;i<n;i++) scanf("%d", &a[i]);

    int hh=0, tt=-1;
    for(int i=0;i<n;i++){
        if(hh<=tt && q[hh] <i-k+1) hh++;

        while(hh<=tt && a[q[tt]] >= a[i]) tt--;
        q[++tt]=i;

        if(i>=k-1) printf("%d ", a[q[hh]]);
    }
    puts("");

    hh=0, tt=-1;
    for(int i=0;i<n;i++){
        if(hh<=tt && q[hh] <i-k+1) hh++;

        while(hh<=tt && a[q[tt]] <= a[i]) tt--; //求最大值，修改处 
        q[++tt]=i;

        if(i>=k-1) printf("%d ", a[q[hh]]);
    }
    puts("");
}