本题告诉我们：

边上存的信息是很灵活的，除了存边权，还能存各种会影响更新的其他信息

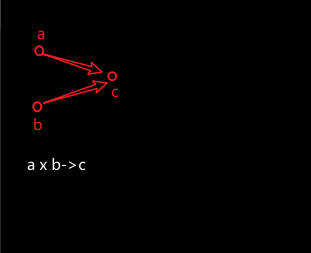
a–(w,b)–>c , b–(w,a)–>c

需要记录在边上的信息不仅包括边权w[i]=max(t[a],t[b])，
还包含与该点配种的植物编号,用g[]存，则更新方式为：

d[j]=min(d[j],max(d[t],d[g[i]])+w[i])

这样就转换为最短路问题了
考虑几个问题
1.能不能用dijk做？
经过验证发现是可行的，因为边权都是正数，每次选取的d最小的点不可能再被其他d比它大的点更新
2.能不能处理有环的情况？
因为求最短路，而各边权为正，不可能存在负环，所以可以处理有环情况，dijk即可
3.能不能用dp做？

dp的思路是记忆化搜索型树形DP
边上存的信息是杂交得到该点的两子节点编号，状态更新：
d[u]=min(d[u],max(t[ee[i].a],t[ee[i].b])+max(dfs(ee[i].a),dfs(ee[i].b)));

因为该图不能保证是树，有可能存在环路，所以不能DP

dijk代码

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;

typedef pair<int,int> pii;
const int N=2010,M=2e5+10;
int n,m;
int e[M],ne[M],w[M],idx,h[N],g[M];
int t[N],a[N],cnt,d[N];
bool st[N];
int ed;

void add(int a,int b,int c){//a->c(边上为b)
    e[idx]=c,w[idx]=max(t[a],t[b]),g[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void dijk(){
    priority_queue<pii,vector<pii>,greater<pii>> q;
    for(int i=1;i<=cnt;i++){
        d[a[i]]=0;
        q.push({0,a[i]});
    }
    while(q.size()){
        auto item=q.top();
        q.pop();
        int t=item.second;
        if(st[t])continue;
        st[t]=true;
        for(int i=h[t];~i;i=ne[i]){
            int j=e[i];
            if(d[j]>max(d[t],d[g[i]])+w[i]){
                d[j]=max(d[t],d[g[i]])+w[i];
                q.push({d[j],j});
            }
        }
    }
}

int main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    memset(h,-1,sizeof h);
    cin>>n>>cnt>>m>>ed;
    for(int i=1;i<=n;i++)cin>>t[i]; 
    for(int i=1;i<=cnt;i++)cin>>a[i];
    for(int i=1;i<=m;i++){
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c),add(b,a,c);
    }
    int ans=0x3f3f3f3f;
    memset(d,0x3f,sizeof d);
    dijk();
    cout<<d[ed];
    return 0;
}

spfa代码

#include <iostream>
#include <cstring>
using namespace std;

const int N=2010,M=2e5+10;
int n,m;
int e[M],ne[M],w[M],idx,h[N],g[M];
int t[N],a[N],cnt,d[N];
bool st[N];
int ed;
int q[N],hh,tt;

void add(int a,int b,int c){//a->c(边上为b)
    e[idx]=c,w[idx]=max(t[a],t[b]),g[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void spfa(){
    for(int i=1;i<=cnt;i++){
        d[a[i]]=0;
        q[tt++]=a[i];
        if(tt==N)tt=0;
        st[a[i]]=true;
    }
    while(hh!=tt){
        int t=q[hh++];
        st[t]=false;
        if(hh==N)hh=0;
        for(int i=h[t];~i;i=ne[i]){
            int j=e[i];
            if(d[j]>max(d[t],d[g[i]])+w[i]){
                d[j]=max(d[t],d[g[i]])+w[i];
                if(!st[j]){
                    st[j]=true;
                    q[tt++]=j;
                    if(tt==N)tt=0;
                }
            }
        }
    }
}

int main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    memset(h,-1,sizeof h);
    cin>>n>>cnt>>m>>ed;
    for(int i=1;i<=n;i++)cin>>t[i]; 
    for(int i=1;i<=cnt;i++)cin>>a[i];
    for(int i=1;i<=m;i++){
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c),add(b,a,c);
    }
    int ans=0x3f3f3f3f;
    memset(d,0x3f,sizeof d);
    spfa();
    cout<<d[ed];
    return 0;
}