题目描述

假设有一个非常长的数轴，数轴长度为$-10^9$~$10^9$之间，每个位置上所存储的值都为$0$。

现在要向其中大约$10^5$个位置上插入某个数

最后要向该数轴进行若干次询问，查询方式是以区间的方式进行，要求输出位于该区间的所以坐标存储的总数值

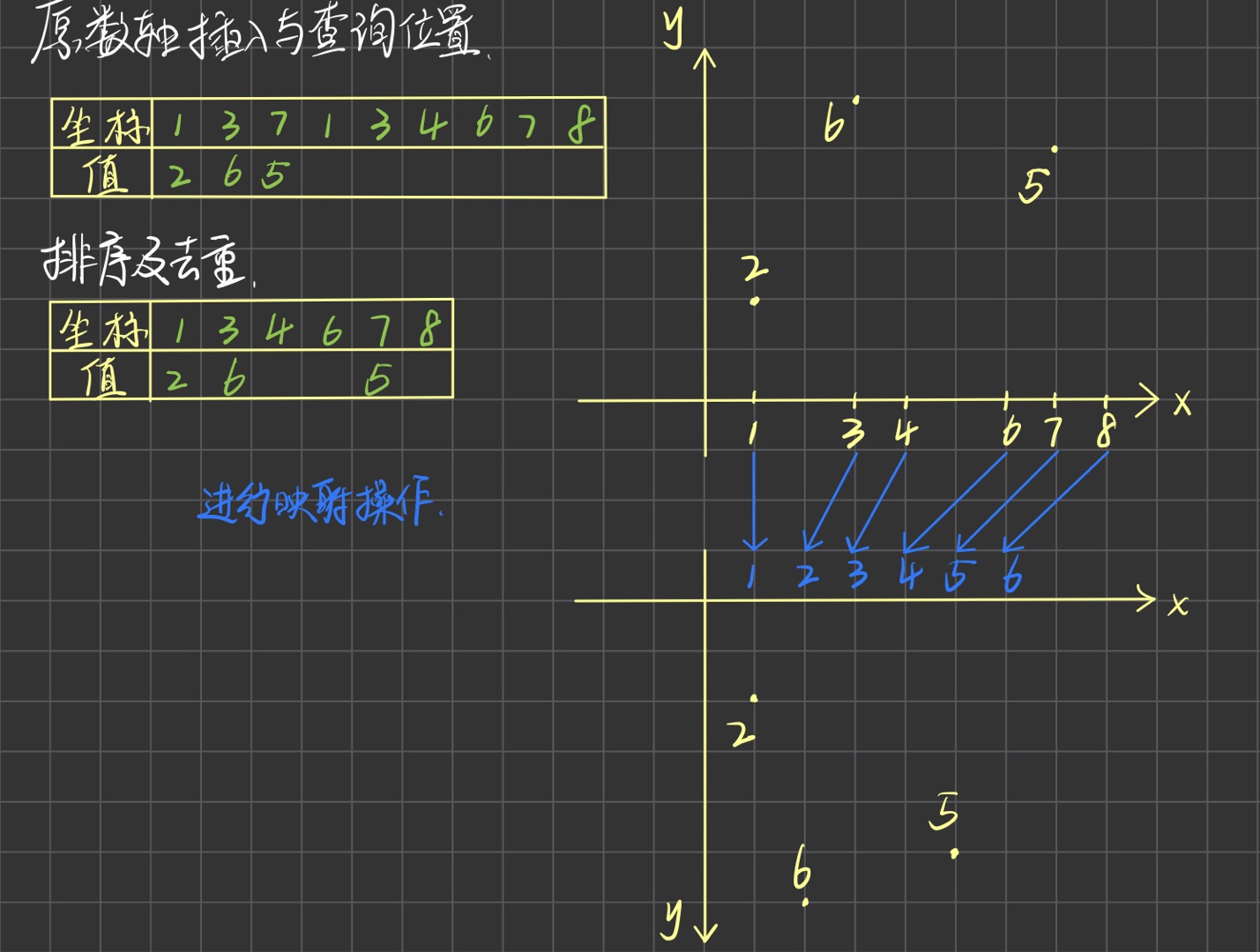
首先我们发现插入数值和查询的过程中，插入位置和查询位置并非是按照位置的大小次序排列的，所以我们要对插入位置和查询位置坐标大小进行排序，顺便进行对重复位置的去重，同时可以便于我们在后续查询的过程中直接利用前缀和公式 $S[r]-S[l-1]$。

数轴分布的长度远远大于区间插入数所在位置的个数，未插入数的坐标上所存储的值都为$0$。因此我们可以通过某种函数或映射关系，将数轴缩短，使得原数轴存储值非$0$的位置，和查询的位置映射到新数轴上。最关键的是要在这个过程中数轴坐标之间的位置大小关系保持不变。

寻找这种映射关系最简单直接的方法就是将每个插入位置和查询位置存在一个数组里，通过对重复位置的去重操作，我们已经得到了插入位置和查询位置和数组下标的一一对应关系，通过这种关系将原数轴缩短。

这就是所谓的整数保序离散化。

C++ 代码

#include<bits/stdc++.h>

using namespace std;

const int N=3e5+10; //插入操作和查询操作数据量的上界
int a[N]; //存储坐标所对应的值
int s[N]; //对a数组的前缀和数组
vector<pair<int,int>> add,query;
//add可以存储插入过程中所在坐标和对应的值
//query可以存储查询过程中的区间端点
vector<int> alls; //将插入位置和查询位置的区间端点位置存储在数组中，便于利用数组下标离散化

int find(int item) //返回映射的位置也就是去重排序后alls数组下标
{
    int l=0,r=alls.size()-1;
    while(l<r)
    {
        int mid=l+r>>1;
        if(alls[mid]>=item) r=mid;
        else l=mid+1;
    }
    return r+1; //前缀和一般要让数组下标从1开始
}

int main()
{
    int n,m;
    scanf("%d%d",&n,&m);

    while(n--)
    {
        int x,c;
        scanf("%d%d",&x,&c);
        add.push_back({x,c});
        alls.push_back(x);
    }

    while(m--)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        query.push_back({l,r});
        alls.push_back(l);
        alls.push_back(r);
    }

    sort(alls.begin(),alls.end());  //排序
    alls.erase(unique(alls.begin(),alls.end()),alls.end()); //去重

    for(auto item:add)
    {
        int x=find(item.first);
        a[x]+=item.second;
    }

    for(int i=1;i<=alls.size();i++) s[i]=s[i-1]+a[i];  //前缀和

    for(auto item:query) //处理询问
    {
        int l=find(item.first);
        int r=find(item.second);
        cout<<s[r]-s[l-1]<<endl;
    }

    return 0;
}

Reference

AcWing 802. 画个图辅助理解~
看了这个大佬的题解，大家可以看看他的