题目描述
X星球的考古学家发现了一批古代留下来的密码。
这些密码是由A、B、C、D 四种植物的种子串成的序列。
仔细分析发现,这些密码串当初应该是前后对称的(也就是我们说的镜像串)。
由于年代久远,其中许多种子脱落了,因而可能会失去镜像的特征。
你的任务是:
给定一个现在看到的密码串,计算一下从当初的状态,它要至少脱落多少个种子,才可能会变成现在的样子。
样例
输入样例1:
ABCBA
输出样例1:
0
输入样例2:
ABDCDCBABC
输出样例2:
3
算法
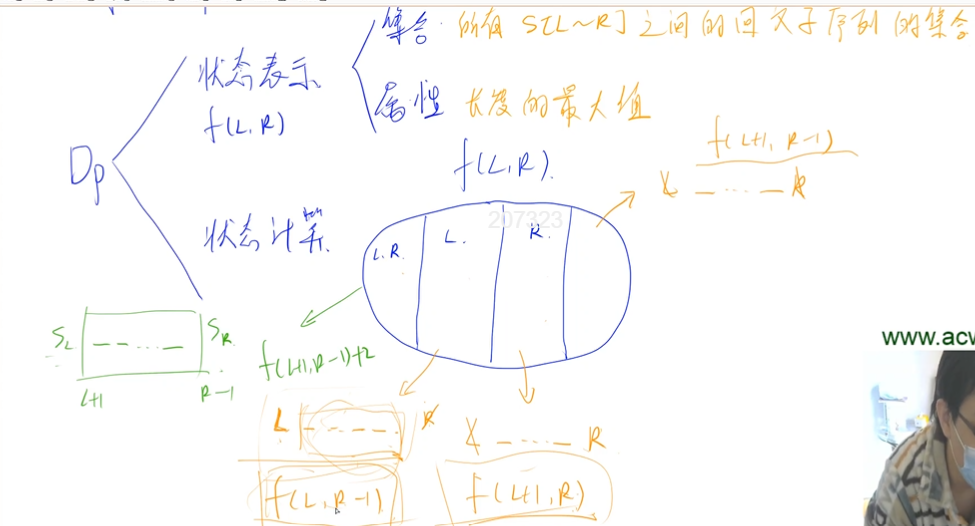
(区间dp) 可参考最长公共子序列
求最长回文子序列
重点是会分析以及有思路。。其实很有意思。。
从初始状态变成当前状态需要脱落叶子的数量等价于当前样子变成最大的回文串需要剪去的叶子的数量。
时间复杂度
参考文献
C++ 代码
#include<iostream>
using namespace std;
const int N=1010;
int f[N][N];
int main()
{
string s;
cin>>s;
int n=s.size();
for(int len=1;len<=n;len++)//因为l要用到l+1的值,所以先枚举序列长度更好。
for(int l=0;l+len-1<n;l++)
{
int r=l+len-1;
if(len==1)
f[l][r]=1;
else
{
f[l][r]=max(f[l+1][r],f[l][r-1]);
if(s[l]==s[r])
f[l][r]=max(f[l][r],f[l+1][r-1]+2);
}
}
cout<<n-f[0][n-1]<<endl;
return 0;
}

