算法分析：

这也是一个较为经典的状态机DP问题，因为仅仅用选择这个职员或者不选择这个职员是无法完整的表达出各种情况的，因为这里存在不能和顶头上司（父节点）同时出现的限制。

这里同时复习了树的存储与插入等操作。

手动加深递归上限：

注：python对于递归的深度有一定的限制，一般认为递归的深度（次数）不超过1000，对于一些需要递归比较深层次的题目，需要手动加深递归的上限。
代码如下：

import sys
sys.setrecursionlimit(6000)

树的存储与插入：

利用单列表来存储树，每次添加一条边。
需要用到h[N]用来存储头结点，初始化为- 1
e[N]存储每个结点
ne[N]用来存储每个结点的next指针
idx是空的位置，所以每次最后要+=1（注意在add函数中要设为global）

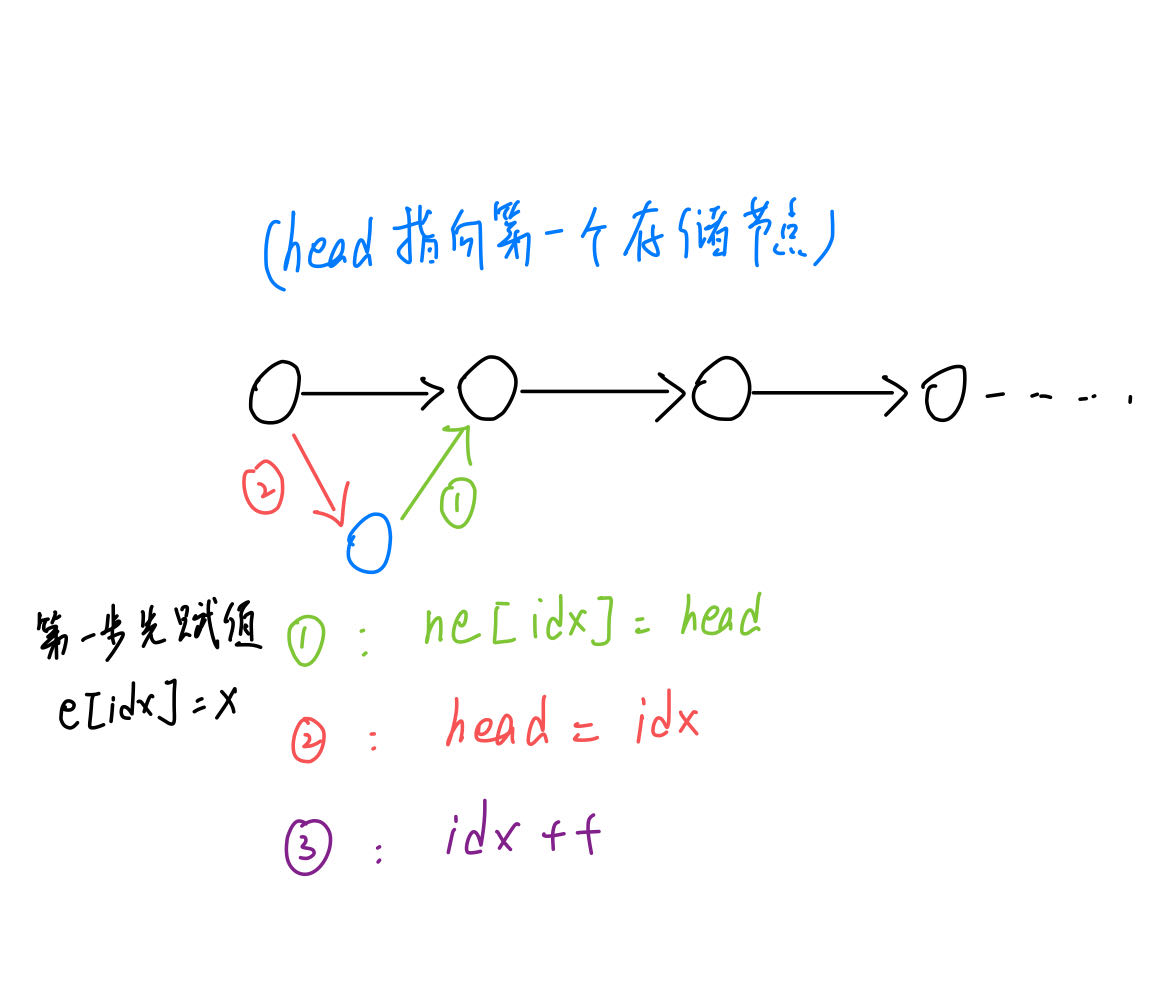
添加边的过程（头插法）：

def add(a, b):
    global idx
    e[idx] = b
    ne[idx] = h[a]
    h[a] = idx
    idx += 1

动态规划：

• 状态表示$f[i][j]$：
  f[i][0]：在以i为结点的子树中选择，且不选择i这个点的方案的集合
  f[i][1]：在以i为结点的子树中选择，且选择i这个点的方案的集合
• 集合属性：$Max$
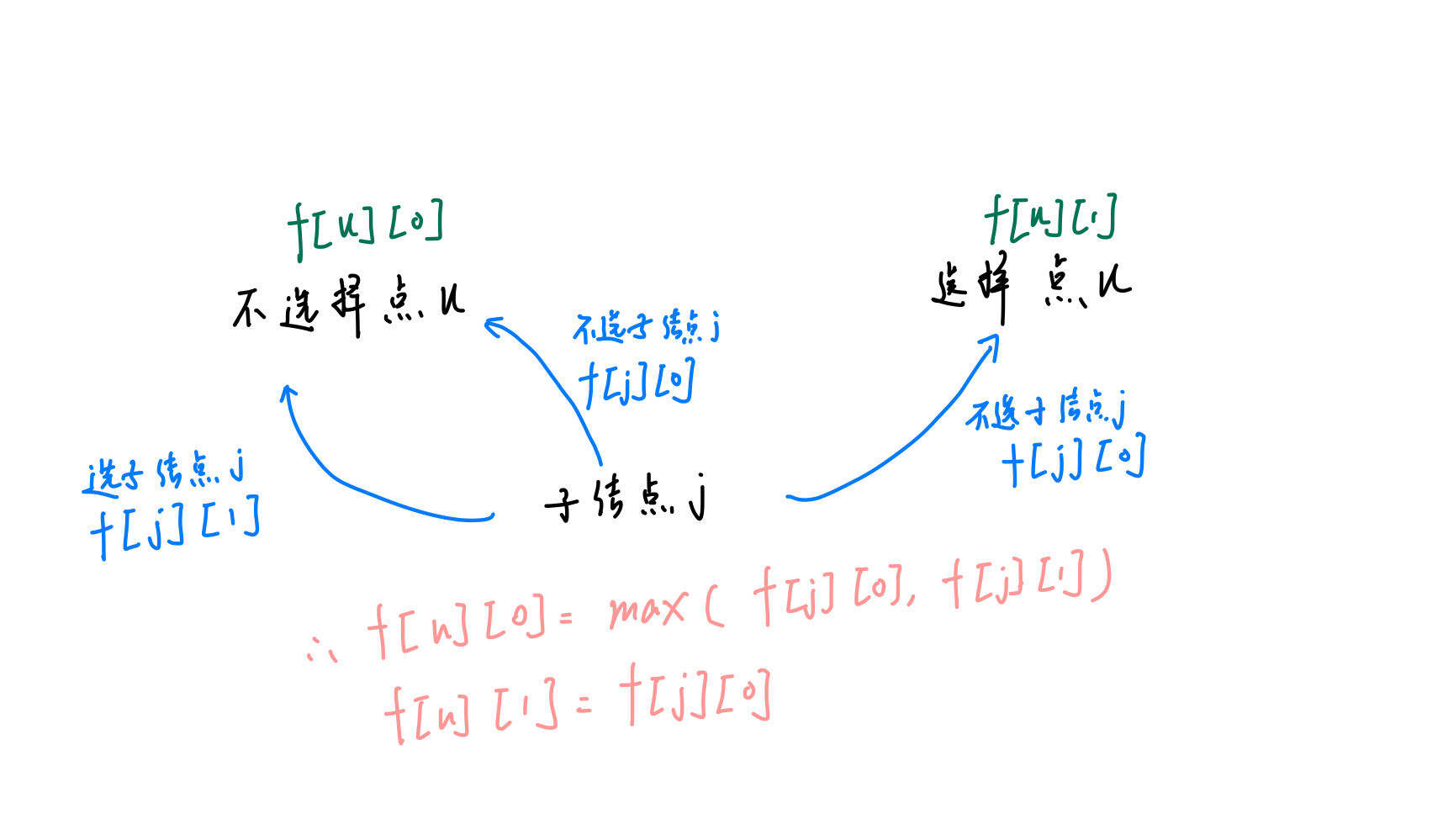
• 状态计算：这里j是i的子结点
  f[u][0] += max(f[j][0], f[j][1]) 不选这点，那么子节点可选可不选，取较大值
  f[u][1] += f[j][0] 选这个点，那么不能取子节点

状态机图示：

初始状态：
从根节点开始递归计算即可，好像没有非法状态，就不用设置无穷大了，全部初始化为0。

目标状态：
f[root][0]和f[root][1]中的较大值

时间复杂度：$O(N)$ （每个点算一次）

py 代码

import sys
input = lambda:sys.stdin.readline().rstrip()
sys.setrecursionlimit(6000)
N = 6010
happy = [0] * N
f = [[0] * 2 for i in range(N)]
h = [- 1] * N
e = [0] * N
ne = [0] * N
has_father = [False] * N
idx = 0

def add(a, b):
    global idx
    e[idx] = b
    ne[idx] = h[a]
    h[a] = idx
    idx += 1


def dfs(u):
    f[u][1] = happy[u]
    i = h[u]
    while  i != -1:
        j = e[i]
        dfs(j)

        f[u][0] += max(f[j][0], f[j][1])
        f[u][1] += f[j][0]

        i = ne[i]


n = int(input())
for i in range(1, n + 1):
    happy[i] = int(input())

for i in range(n - 1):
    a, b = map(int, input().split())
    add(b, a)
    has_father[a] = True

root = 1
while has_father[root] == True:
    root += 1

dfs(root)

print(max(f[root][1], f[root][0]))