原题连接

题目描述

有一个$m \times m$的棋盘，棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。

任何一个时刻，你所站在的位置必须是有颜色的（不能是无色的）， 你只能向上、 下、左、 右四个方向前进。当你从一个格子走向另一个格子时，如果两个格子的颜色相同，那你不需要花费金币；如果不同，则你需要花费 $1$个金币。

另外， 你可以花费 $2$ 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用， 而且这个魔法的持续时间很短，也就是说，如果你使用了这个魔法，走到了这个暂时有颜色的格子上，你就不能继续使用魔法； 只有当你离开这个位置，走到一个本来就有颜色的格子上的时候，你才能继续使用这个魔法，而当你离开了这个位置（施展魔法使得变为有颜色的格子）时，这个格子恢复为无色。

现在你要从棋盘的最左上角，走到棋盘的最右下角，求花费的最少金币是多少？

输入输出格式

输入格式：

第一行包含两个正整数$m, n$，以一个空格分开，分别代表棋盘的大小，棋盘上有颜色的格子的数量。

接下来的$n$行，每行三个正整数$x, y, c$， 分别表示坐标为$(x,y)$的格子有颜色$c$。

其中$c=1$ 代表黄色，$c=0$ 代表红色。 相邻两个数之间用一个空格隔开。 棋盘左上角的坐标为$(1, 1)$，右下角的坐标为$( m, m)$。

棋盘上其余的格子都是无色。保证棋盘的左上角，也就是$(1, 1)$ 一定是有颜色的。

输出格式：

一个整数，表示花费的金币的最小值，如果无法到达，输出$-1$。

输入输出样例

输入样例#1：

复制

5 7
1 1 0
1 2 0
2 2 1
3 3 1
3 4 0
4 4 1
5 5 0

输出样例#1：

8

输入样例#2：

5 5
1 1 0
1 2 0
2 2 1
3 3 1
5 5 0

输出样例#2：

-1

说明

输入输出样例 1 说明

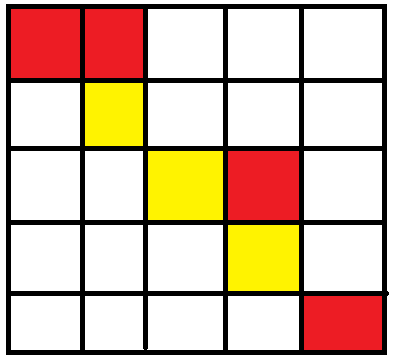
从$(1,1)$开始，走到$(1,2)$不花费金币

从$(1,2)$向下走到$(2,2)$花费 $1$ 枚金币

从$(2,2)$施展魔法，将$(2,3)$变为黄色，花费 $2$ 枚金币

从$(2,2)$走到$(2,3)$不花费金币

从$(2,3)$走到$(3,3)$不花费金币

从$(3,3)$走到$(3,4)$花费 $1$ 枚金币

从$(3,4)$走到$(4,4)$花费 $1$ 枚金币

从$(4,4)$施展魔法，将$(4,5)$变为黄色，花费$2$ 枚金币，

从$(4,4)$走到$(4,5)$不花费金币

从$(4,5)$走到$(5,5)$花费 $1$ 枚金币

共花费 $8$枚金币。

输入输出样例 2 说明

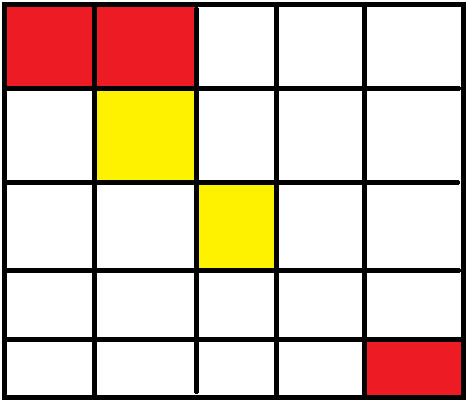
从$( 1, 1)$走到$( 1, 2)$,不花费金币

从$( 1, 2)$走到$( 2, 2)$,花费$1$金币

施展魔法将$( 2, 3)$变为黄色,并从$( 2, 2)$走到$( 2, 3)$花费$2$ 金币

从$( 2, 3)$走到$( 3, 3)$不花费金币

从$( 3, 3)$只能施展魔法到达$( 3, 2),( 2, 3),( 3, 4),( 4, 3)$

而从以上四点均无法到达$( 5, 5)$,故无法到达终点,输出$-1$

数据规模与约定

对于 $30\%$的数据, $1 \le m \le 5, 1 \le n \le 10$。

对于 $60\%$的数据, $1 \le m \le 20, 1 \le n \le 200$。

对于 $100\%$的数据, $1 \le m \le 100, 1 \le n \le 1,000$。

解题报告

题意理解

这道题目的一句话题意是:

让你从$(1,1)$走到$(m,m)$,要求路上的花费代价最少.
如果你从A走到B,那么走一步的代价有三种:
1. 若方格A的颜色等于方格B的颜色,那么花费代价为0
2. 若方格A的颜色不同于方格B的颜色,那么花费代价为1.
3. 若方格B的颜色为无色,那么相当于使用一次魔法,且花费的代价为2,并且下一步不可以使用魔法.

判断算法

一般来说,我们面对类似于迷宫这类,也就是具有非常明确的图像显示的题目,而言我们需要第一时间思考到这道题目是不是要用到搜索算法

算法选择

搜索的算法有很多种.比如说深度优先搜索,广度优先搜索,A搜索,IDA搜索,但是对于$m \le 100$的数据范围,而言我们并不需要多么高级的搜索,只需要一点点记忆化剪枝+深度优先搜索即可

思路确定

首先对于一道搜索题目而言的话,我们有基本的三点目标

目标一:方向指示数组,这个数组在迷宫问题中,你可以认为是走路方式,在动态规划问题中,你可以认为是拓展状态的决策.

目标二:边界处理,对于这道题目而言,边界处理其实很简单,就是在指定的区域里面而已.也就是 $(x,y)$ 不越界

目标三:拓展准则,一道题目而言我们不仅仅要满足边界处理,还有更为重要,也就是这道题目的最重要的一点,如何判断我们走这一步是满足条件的.以及这一步花费的代价

细节处理

目标三处理是我们这道题目的核心关键,也就是不同于其他问题的一个难点.下面我会详细的说明.

1. 上一次使用了魔法,那么这一次不能使用魔法
2. 上一次使用了魔法,判断上一个点是不是和当前点颜色一致
3. 颜色相同则不需要花费代价,否则花费1点代价
4. 拓展的点是无颜色,那么我们必须使用魔法,并且花费两点代价

代码演示

#include <bits/stdc++.h>
using namespace std;
const int N=1100;
const int dx[4]= {1,-1,0,0};
const int dy[4]= {0,0,1,-1};
int g[N][N],n,m,dis[N][N],vis[N][N],ans=1e9;
int check(int x,int y)
{
    if (x<1 || x>n || y<1 || y>n || vis[x][y])//在合法的矩阵内部,而且没有访问
        return true;//一个条件不满足,则这一步无法拓展.
    return false;
}
void dfs(int x,int y,int nowc,int r)
{
    if(x==n && y==n && r<ans)
    {
        ans=r;
        return;
    }
    if(r>=dis[x][y])//如果发现当前的代码,已经大于上一次我来到这个点的代价,那么显然可以剪枝,我再怎么最优,也没有上一次最优.
        return;
    dis[x][y]=r;//记录最优值
    for(int i=0; i<4; i++)//四个拓展步骤
    {
        int xx=x+dx[i],yy=y+dy[i],cl=g[xx][yy];//拓展步骤,并且看下一步的颜色
        if (check(xx,yy))//如果不越界,而且没有走过这个点的话
            continue;
        vis[xx][yy]=true;//已经访问了
        if(nowc>=3 && cl!=0)//如果说上一次使用了魔法,但是我当前这个点不需要使用魔法的话
        {
            if((nowc+cl)%2==0)//这一步非常重要,大致意思是,这两个点颜色相同,或者上一次魔法和本宫格颜色一样.
                dfs(xx,yy,cl,r);//不需要花费代价
            else
                dfs(xx,yy,cl,r+1);//需要花费代价
        }
        else if(nowc==1 || nowc==2)//如果这个上一次没有使用魔法的话
        {
            if(cl==1 || cl==2)//当前宫格不需要使用魔法
            {
                if(nowc!=cl)//颜色不一样
                    dfs(xx,yy,cl,r+1);
                else//颜色一样
                    dfs(xx,yy,cl,r);
            }
            else
                dfs(xx,yy,nowc+2,r+2);//使用魔法
        }
        vis[xx][yy]=false;//回溯处理.
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>n>>m;
    memset(dis,0x3f,sizeof(dis));
    for(int i=1; i<=m; i++)
    {
        int x,y,c;
        cin>>x>>y>>c;
        g[x][y]=c+1;//习惯颜色处理.
    }
    vis[1][1]=true;//初始点已经访问了
    dfs(1,1,g[1][1],0);//开始搜索
    if (ans==1e9)//找不到合法方案
        cout<<-1;
    else
        cout<<ans;/找到了
    return 0;
}