算法分析
-
将所有区间按照左端点从小到大进行排序
-
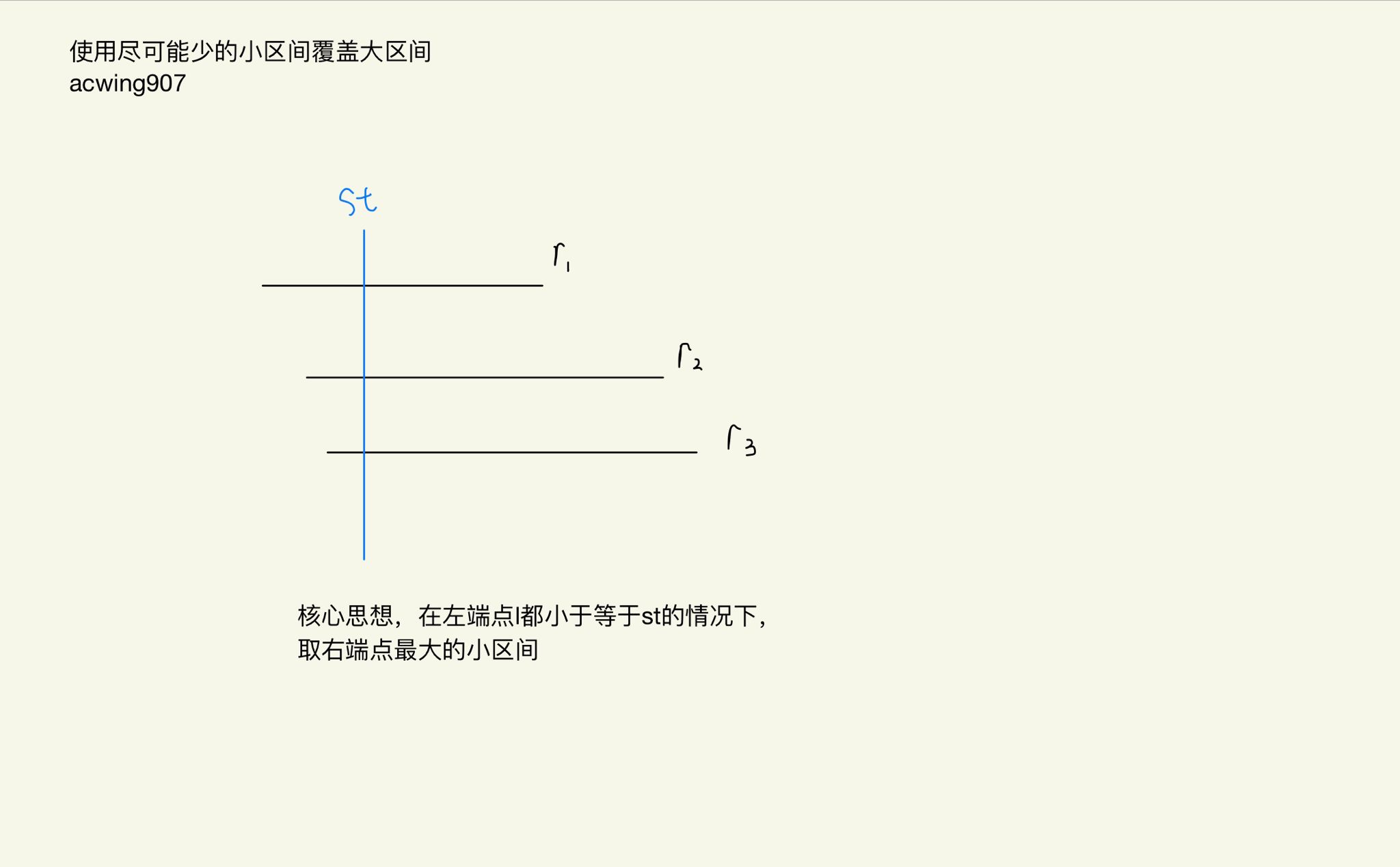
从前往后枚举每个区间,在所有能覆盖
start的区间中,选择右端点的最大区间,然后将start更新成右端点的最大值这一步用到了
贪心决策
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
struct Range
{
int l, r;
bool operator< (const Range &W)const
{
return l < W.l;
}
}range[N];
int main()
{
int st, ed;
scanf("%d%d", &st, &ed);
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
{
int l, r;
scanf("%d%d", &l, &r);
range[i] = {l, r};
}
sort(range, range + n);
int res = 0;
bool success = false;
for (int i = 0; i < n; i ++ )
{
int j = i, r = -2e9;
while (j < n && range[j].l <= st)
{
r = max(r, range[j].r);
j ++ ;
}
if (r < st)
{
res = -1;
break;
}
res ++ ;
if (r >= ed)
{
success = true;
break;
}
st = r;
i = j - 1;
}
if (!success) res = -1;
printf("%d\n", res);
return 0;
}

想问一下大佬r = -2e9放在循环外面为什么会tle但是放在循环里面却可以过
每次都要更新 r 的值
每次都要将r的值置为-2e9,如果在外面只赋值了一次。
主要是max哪里出问题了
。。我为什么要评论四次?????
好的,谢谢大佬,我自己也发现样例了
4 10 2
4 5
11 12
这个样例就比较能够说明问题
因为评论不要钱hh
??原谅我还是有点懵,能详细一点吗 谢谢大佬♪(・ω・)ノ
例如样例:
4 10 2
4 5
11 12
当第一轮st更新后是5,第二轮j 还是 0,不过此时应该退出了,但如果-2e9放在外面,
if (r < st)
{
res = -1;
break;
}
就不会执行
谢谢大佬orz,后面我
debug搞懂了hh这样例确实强
hhhh这小问题卡了一个半小时,没想出来怎么tle的
兄弟,不太对吧,感觉第二轮j应该是1了吧,第一轮的话j=1,然后i=j-1,为0了,然后i++,i又成1了,j=i,j应该是1了吧
如果r = -2e9放在循环的外面,那么进入while循环的时候,r=st,若存在最大的r小于st的情况,经过while循环之后,r仍然是st,那么就永远都不会进入if(r < st),此时if(r>st)的条件也不满足,success的值永远都是false,就只有等待整个for循环结束,然后最后的一个if语句,导致了res=-1,然后你就会发现wrong answer
r=-INF放在循环内而不是循环外的原因:
如果r放在循环外,在for循环至少循环一次后,下一次循环开始r是与st相等的,如果在这个循环中while遍历的第一个区间左端点值大于st,也就意味着小区间不能完全覆盖大区间,这时本应该执行r<st的break,并输出-1,但由于while遍历的第一个区间左端点值大于st,不执行r = max(r, range[j].r);,r还是等于st,此时不会执行r<st的break,于是进入了死循环,自然会TLE
样例:
1 5
2
1 2
4 5
由于j永远不会进入while循环更新,所以每次for结束的时候j都是1,i也都是0,相当于永远在循环遍历第1个元素
在循环中的res=-1多余了,
对的
同学们加油 hhh
你好,“y总”
你的hh不对(应该是hh~)(机智)
为什么视频题解里i要更新啊,i=j-1,一直没明白
我也在纠结额,不加也能AC
加了之后就不用考虑那些“不贪心”的区间了,即除了贪心区间之外的其他
左端点小于L的区间,因为他们的右端点不够贪心(最大)为什么i = j-1啊 是因为 for的i++么?
嗯
感觉不需要i=j-1, 直接i=j也能过
i=j过不了,如果i=j的时候,这时候已经拿的是下一个区间来比较了,但是不要忘记i在for循环里,最后还要+1,所以如果i=j的话,相当于跳过了一个区间,所以只能i=j-1
get it! thank u~
比如第一次时,while遍历所有的左端点比st小的区间,此时答案应该为j-1,比如答案为j=4时,但j=4这个区间我没用,所以我要i=j-1
为什莫i = j是下一个空间啊!!!
I do not get it…
就是说 while (j < n && range[j].l <= st)//小于等于左边界
{
r = max(r, range[j].r);//不断更新右端点
j ;
}这个执行后,j会跳到下一个没有遍历的点,如果i=j,然后有会进行i,那么就会直接跳过j+1,从第j+2个点开始遍历,因为i还会再for循环更新
i=j-1,在for又会+1,正好到第j个啦懂了懂了
orZ
可以,想了半天,感谢!
从答主学来的思路,代码写起来简洁一些
#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 10; struct range_t { int l, r; bool operator< (range_t &other) const { return l < other.l; } }; int n, a, b, s, t; range_t rg[N]; int main() { cin.tie(0); cin >> s >> t; cin >> n; for (int i = 0; i < n; i ++) { cin >> a >> b; rg[i] = {a, b}; } sort(rg, rg + n); int res = 0, cur_r = -2e9, max_r = -2e9, idx = 0; while (cur_r < t) { int max_l = (cur_r == -2e9 ? s : cur_r); for (; idx < n && rg[idx].l <= max_l; idx ++) max_r = max(max_r, rg[idx].r); if (max_r == cur_r) break; res ++; cur_r = max_r; } if (cur_r < t) cout << -1 << endl; else cout << res << endl; return 0; }没太搞懂这道题双指针体现在哪里
for (int i = 0; i < n; i )
{
int j = i, r = -2e9;
while (j < n && range[j].l <= st)
{
r = max(r, range[j].r);
j ;
}
这里就是双指针啊,枚举每一个区间,在区间都能覆盖st点的情况下,选区间右端点最大的区间
就代码直接翻译就是如果我包含st这个点,那就j++看下一个区间,直到看到不包含st的区间截止
体现在左端点不是从0-n进行遍历,依靠内部的while循环更新j,最后i会跳过j遍历过的点
我觉y 总的代码有一点问题:st = r 应该改成 st = r + 1, 因为 r 使我们当前已经能覆盖到的,那些下次我们至少需要覆盖到的位置是 st=r+1 位置,,,,,,,,,,,,,,,,这题的倒数第二组数据有问题。。。。。。。
st=r,当i从j-1开始枚举,找到比st要小的左端点,要是st=r+1,如果我只找到左端点为r+1,那么此时 线段区间中的(r,r+1)没有覆盖,所以肯定是等于r呀
已经明白了,谢谢大佬指正。
嗯嗯,这里是从j开始枚举。。。
感谢
分享一个我认为更加优雅的解法:
#include <bits/stdc++.h> #include <iomanip> using namespace std; using ll = long long; using ull = unsigned long long; using ii = pair<int, int>; using iii = tuple<int, int, int>; int main(){ int n, s, t, a, b; cin >> s >> t >> n; vector<ii> inters; for (int i = 0; i < n; i++){ cin >> a >> b; inters.push_back({a, b}); } sort(inters.begin(), inters.end()); int res = 0, ok = 0; for (int i = 0; i < n; i++){ // 必须注意: 只有 inters[i] 左侧断点小于s 才能进入分组循环 if(inters[i].first <= s){ int bg = i, rmost = inters[i].second; while (i + 1 < n && inters[i + 1].first <= s){ rmost = max(rmost, inters[i + 1].second); i++; } res++; if ((s = rmost) >= t){ ok = 1; break; } } } cout << (ok ? res: -1) << endl; return 0; }看起来这是分组循环的解法
复杂度为什么不是O(n^2)
因为这里对于区间已经排好序了,双指针在这里是具有单调性的,时间复杂度从n方降到n了
仅用一个下标 i 也可以完成遍历,感觉更好理解一点。
#include [HTML_REMOVED]
#include [HTML_REMOVED]
using namespace std;
const int N =100010;
typedef pair[HTML_REMOVED] PII;
int st,ed;
int n;
PII p[N];
int main()
{
cin >> st >> ed;
cin >> n;
for(int i=0;i[HTML_REMOVED]> a >> b;
p[i] = {a,b};
}
sort(p,p+n);
int i = 0,res = 0; bool flag = false; while(i < n) { int r = -2e9; while(i<n && p[i].first <= st) { r = max(r,p[i].second); i++; } if(r < st) //找不到能够包含起点st的区间 { res = -1; break; } res++; if(r >= ed) { flag = true; break; } st = r; } if(flag) cout <<res <<endl; else cout << -1 <<endl; return 0;}
想问下大佬们我这里哪里出了错误,为什么在vs能运行成功,但是在提交答案的时候出现了Segmentation Fault的错误
#include<iostream> #include<algorithm> using namespace std; const int N = 100010; struct node { int l, r; }arr[N]; bool cmp(node a, node b) { return a.l < b.l; } int main() { int L, R; cin >> L >> R; int n; cin >> n; int idx = 0; for (int i = 0; i < n; i++) { int l, r; cin >> l >> r; arr[i] = { l,r }; } sort(arr, arr + n, cmp); int ans = 0; int flag = -1e10; int i = 0; while (L < R) { while (arr[i].l <= L) { flag = max(arr[i].r, flag); i++; } L = flag; ans++; } if (ans == 0)cout << -1; else cout << ans; }数组越界了
while(arr[i].l <= L)应该加一个数组边界判断i < n && arr[i].l <= L#include <bits/stdc++.h> using namespace std; typedef pair<int, int> PII; int s, t, a, b, n, cnt; vector<PII> res; int main() { scanf("%d %d", &s, &t); scanf("%d", &n); for (int i = 0; i < n; i ++) { scanf("%d %d", &a, &b); res.push_back({a, b}); } sort(res.begin(), res.end()); int r = -1e9 - 1; for (int i = 0; i < n; i ++) { if (r >= t) { s = r; cnt ++; break; } if (res[i].first <= s and res[i].second > r) r = res[i].second; else if (res[i].first > s) { cnt ++; s = r; r = -1e9 - 1; if (res[i].first <= s and res[i].second > r) r = res[i].second; } if (i == n - 1) { cnt ++; s = r; } } if (s >= t) cout << cnt << endl; else cout << -1 << endl; return 0; }为什么要判断有没有成功呢,直接输出不行吗
无法覆盖线段有两种情况,r<st只判断了一种,
1 5
2
-1 2
2 4
你可以试试这个用例
为什么要按照左端点排序而不是其它呢大佬们
r<st 那为啥要用break呢
这意味着我遍历完了所有左端点小于等于
st的range却依然找不到一个range可以进入st-ed区间,说明至少起点没法覆盖,自然也就没法做到符合题意的区间覆盖,直接res=-1然后break了懂了!
因为不break的话,会死循环。这里就会一直i = i - 1然后i++
如果存在有一段覆盖不到的区域,会死循环。比如 1 10 中 1 4 5 10 那么在第二次时候 i = 1, st = 5, j = 1 -> range[j].l为5 > st 则 i = j - 1 = i - 1进入死循环。
就是说,我们按照左端点排序后,可能区间会存在 间隔,1-2,3-4,第二个区间的左端点大于第一个的右端点,显示无法实现覆盖,直接退出即可
orz