算法分析
-
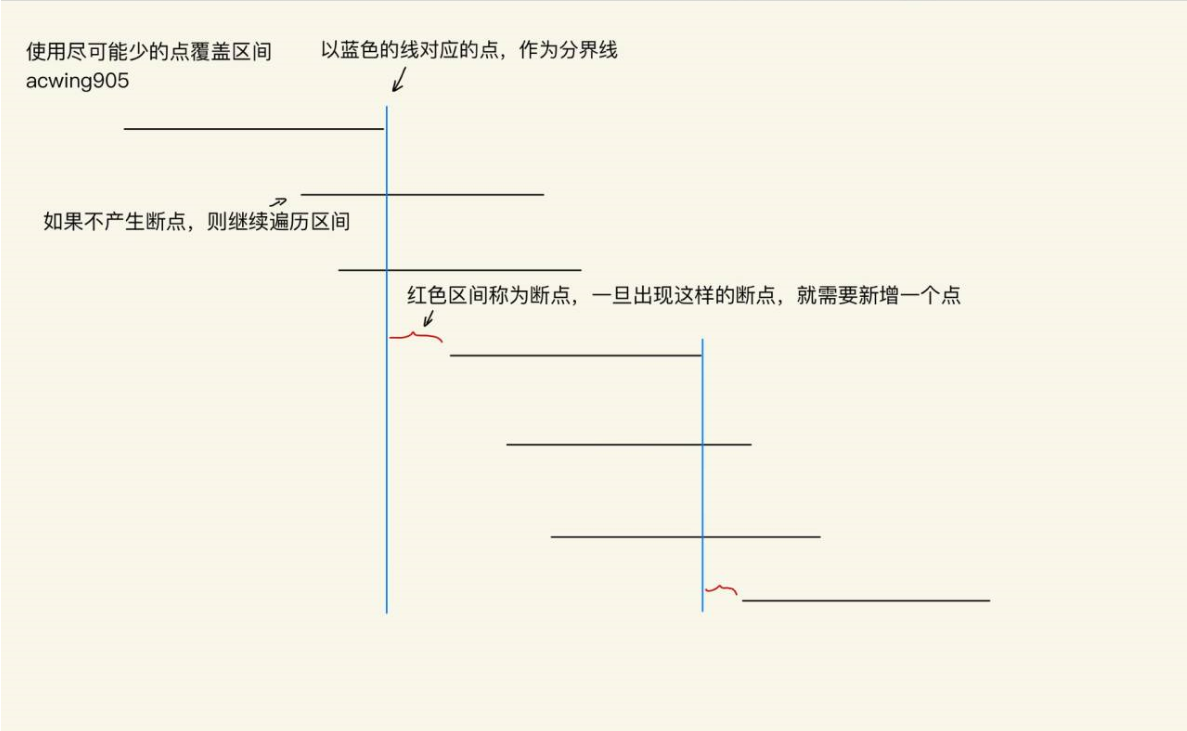
将每个区间按照右端点从小到大进行排序
-
从前往后枚举区间,end值初始化为无穷小
-
如果本次区间不能覆盖掉上次区间的右端点,
ed < range[i].l说明需要选择一个新的点,
res ++ ; ed = range[i].r;
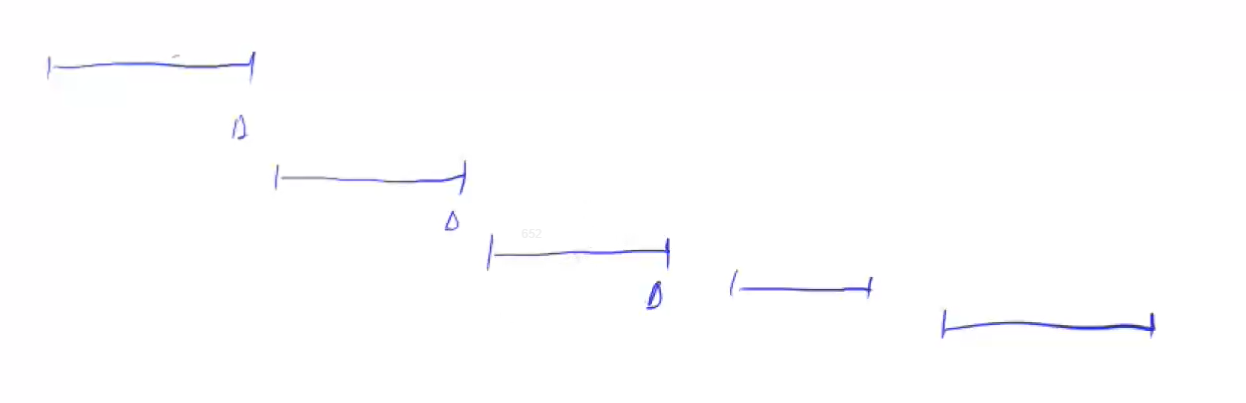
- 如果本次区间可以覆盖掉上次区间的右端点,则进行下一轮循环
-
时间复杂度 O(nlogn)
证明
-
证明
ans<=cnt:cnt是一种可行方案,ans是可行方案的最优解,也就是最小值。 -
证明
ans>=cnt:cnt可行方案是一个区间集合,区间从小到大排序,两两之间不相交。所以覆盖每一个区间至少需要cnt个点。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
struct Range
{
int l, r;
bool operator< (const Range &W)const
{
return r < W.r;
}
}range[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d%d", &range[i].l, &range[i].r);
sort(range, range + n);
int res = 0, ed = -2e9;
for (int i = 0; i < n; i ++ )
if (ed < range[i].l)
{
res ++ ;
ed = range[i].r;
}
printf("%d\n", res);
return 0;
}


大家都证明得很牵强,让我也来证明一下,如果有问题,欢迎指出。疑惑点在ans>=cnt,我们可以假设有ans小于cnt,且咋们用算法求出来的区间用数组t表示。那么这个ans肯定要包含咋们算法求出来的区间。那这个ans可不可能有个区间跨越了咋们求出来的区间t的两个区间呢。显然不可能,这是算法证明的关键。因为如果有这么一个区间的话,咋们贪心算法肯定能找出来,那么t区间就不是咋们算法求解出来的区间了。所以ans连我们数组t都覆盖不了,他还想覆盖全部,简直想屁吃。
反证法确实更好一些
我对你的证明理解是这样的:
假设有ans < cnt,我们的算法求出来的区间(注意这些区间都是两两不相交的)用数组t(因为选的点都是某个区间的右端点,且点都是不同的,因此可以用这个点当做某个区间)表示。那么这个ans中的点肯定要包含我们算法求出来的区间。那这ans个点中是否有一个点,使得在 t 有两个区间都包含这个点呢?显然不可能。我们求出来的区间数量 t 还不是全部的区间数。因此ans>= cnt。
不知道对不对,呵呵
为啥我觉得跟答主写的没啥区别,只是你用了反证而已
`//按左端点好理解一点,但这里如果按右端点排序的话,效果和左端点是一样的, //并且不需要对最右边最小集合(交集)求min, //因为每次交集后的最右边已经按顺序排好了(这很容易看出)` //////////////////////////////////////////////////////////////////////// //以左端点排序 #include <iostream> #include <vector> #include <algorithm> using namespace std; vector<pair<int , int>>a; int n ,nums = 1; int main() { cin >> n; while( n--) { pair<int , int> x; cin>>x.first>>x.second; a.push_back(x); } sort (a.begin() , a.end()); for (int i = 1 , j = 0; i < a.size() ; ++i) { if (a[i].first > a[j].second ) { nums++; j = i;//多个交集以最右边为准 } else { if (a[i].second < a[j].second) j = i; //求min(即该交集的最右边属于那个原集合) } } cout<<nums; return 0; } //以右端点排序 #include <iostream> #include <vector> #include <algorithm> using namespace std; #define pll pair<int ,int> vector<pair<int , int>>a; int n ,nums = 1; bool cmp(pll x , pll y){ return x.second < y.second; } int main() { cin >> n; while( n--) { pll x; cin>>x.first>>x.second; a.push_back(x); } sort (a.begin() , a.end() , cmp); for (int i = 1 , j = 0; i < a.size() ; ++i) { if (a[i].first > a[j].second ) { nums++; j = i;//多个交集以最右边为准 } // else { // if (a[i].second < a[j].second) j = i; //求min(即该交集的最右边属于那个原集合) // } } cout<<nums; return 0; }大佬,我对这里的证明有点疑问,求解。
(1) 证明ans<=cnt 时,你这里的ans指的是可行方案中最少需要的点数;
(2) 证明ans>=cnt 时,你这里的ans指的是可行方案中需要用到的点数。
ans中一个是最少,一个是一般,好像不是指向同一个东西了
这里就证明的很牵强
最优解ans:所有合法方案中的最小值,贪心解cnt
(1)上述选法必然会使每个区间里至少包含一个点,是一种合法方案,所以ans<=cnt
(2)通过贪心方案我们知道序列中包含了cnt个相互之间没有交集的区间,所以对于一个合法方案,必然至少包含cnt个点,所以cnt<=ans
一点拙见
##### 证明:
ans <= cnt :
ans 作为最优解
==反证法:因为ans是由cnt产生的,如果ans>cnt,则ans不是最优解==
ans >= cnt :
ans要覆盖所有的区间
==反证法:因为ans是由cnt产生的,如果ans<cnt,则无法通过cnt产生ans==
这里的sort()实现右端点排序是什么原理,sort()怎么知道是以r为标准排序
因为前面只对结构体的右端点的属性值进行了重载,也就是说只有右端点能进行比较,自然是按照r为标准排序的
而且这里是用结构体类型来存储左右端点,事实上如果直接用pair和vector来存和比较的话是不需要重载运算符的
这里的cnt貌似不是指的一个东西吧
对,感觉cnt的概念变了
对于ans≥cnt的证明:由贪心策略可知,贪心方法将会选择尽量少的点覆盖所有的区间,且每个点对应的区间的集合不相交;使用反证法,不妨假设ans<cnt成立,由于ans是最优解,那么ans个点也覆盖所有的区间,即存在更少的点ans可以覆盖所有的区间。这与贪心策略不符,因为一旦有更少的点可以覆盖所有的区间,那么它一定是贪心解cnt,否则更少的点不能覆盖所有的区间,与假设矛盾。因此ans≥cnt成立
怎么哪都有你!
已经失联好几个月哩
想知道为什么
for(int i = 1 ; i <= n ; i++)这样读入 会Wa掉呢#include <iostream> #include <algorithm> using namespace std; const int N = 1e5+10; struct Section //定义结构体表示每个区间 { int l,r ; bool operator < (const Section &w) const //小于号重载 { return r < w.r; } }section[N]; int main() { int n; cin >> n; for(int i = 1; i <= n; i++) cin >> section[i].l >> section[i].r; sort(section , section + n); //进行排序 int res = 0 ; //表示现在所选的点的个数 int red = -2e9; //表示当前所要选择的区间的上个区间的右端点 for(int i=1 ; i <= n; i++) { if(section[i].l > red) //如果现在的区间和上个区间没有交集 { res++; red = section[i].r; } } cout << res ; return 0; }后面判断那里,你并没有从第一个区间开始遍历
你存的时候没有用零号下表,但是你排序时是从零号下标开始排的,最后一个点没有排序
看到了看到了hh
眼高手低和我一样
#include <bits/stdc++.h> using namespace std; typedef pair<int, int> PII; int n; vector<PII> res; int l, r; int main() { scanf("%d", &n); while (n --) { scanf("%d %d", &l, &r); res.push_back({r, l}); } sort(res.begin(), res.end()); int count = 1, dian = res[0].first; for (int i = 1; i < res.size(); i ++) { if (dian <= res[i].first and dian >= res[i].second) continue; else { count ++; dian = res[i].first; } } cout << count << endl; return 0; }时间复杂度 为什么是O(nlogn)呢?
sort排序的时间复杂度为O(nlogn)
懂了,忽略了这个hh
ok
这个图清楚明白
orz
nb
https://blog.csdn.net/qq_52416556/article/details/136434922?spm=1001.2014.3001.5502 最新图解
#include [HTML_REMOVED]
using namespace std;
vector[HTML_REMOVED]> segs;
vector[HTML_REMOVED]> merges;
int n;
int main() {
cin >> n;
for (int i = 0; i < n; i++) {
int a, b;
cin >> a >> b;
segs.push_back({a, b});
}
sort (segs.begin(), segs.end()); int res = 0; for (int i = 0; i < n; i++) { int L = segs[i][0], R = segs[i][1]; if (i == n-1 || R < segs[i + 1][0]) { res ++; }else { segs[i + 1][0] = max (L, segs[i + 1][0]); segs[i + 1][1] = min (R, segs[i + 1][1]); } } cout << res; return 0;}
用STL
建议用cmp