<算法进阶指南>题解补全计划—进阶指北

此篇属于算法进阶指南题解补全计划—进阶指北收录题解:传送门

题目大意

自然数 拆成 正整数 。正整数可 重复 ，不考虑顺序。至少拆分成 2 个数的和。求方案数。

思路指北

• 一眼完全背包 !
• 将数字看出物品，数字数值就是体积。

• 目标是塞满 体积 n ,没有价值。

• 状态转移方程
  

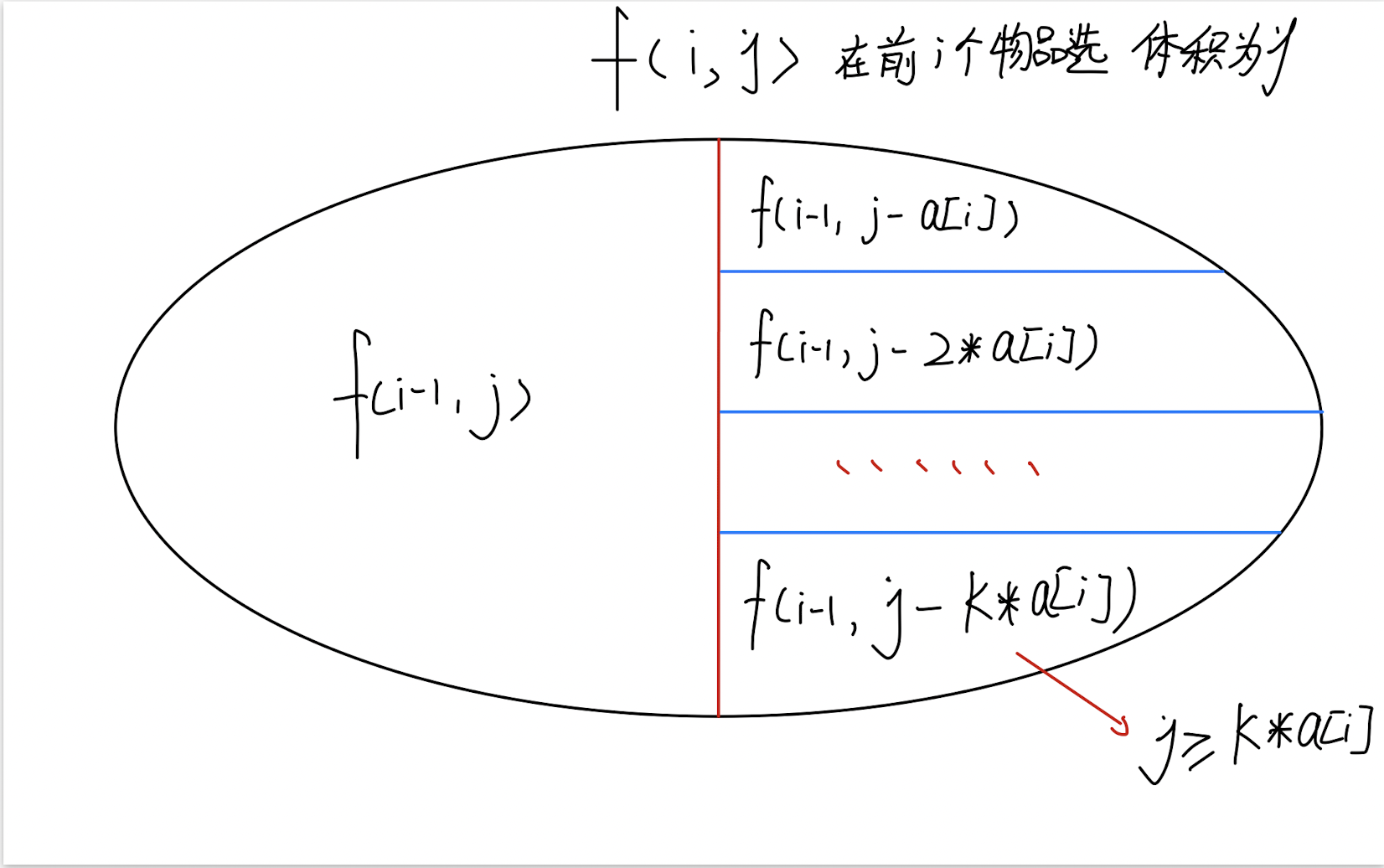
• 方程时间复杂度维度优化

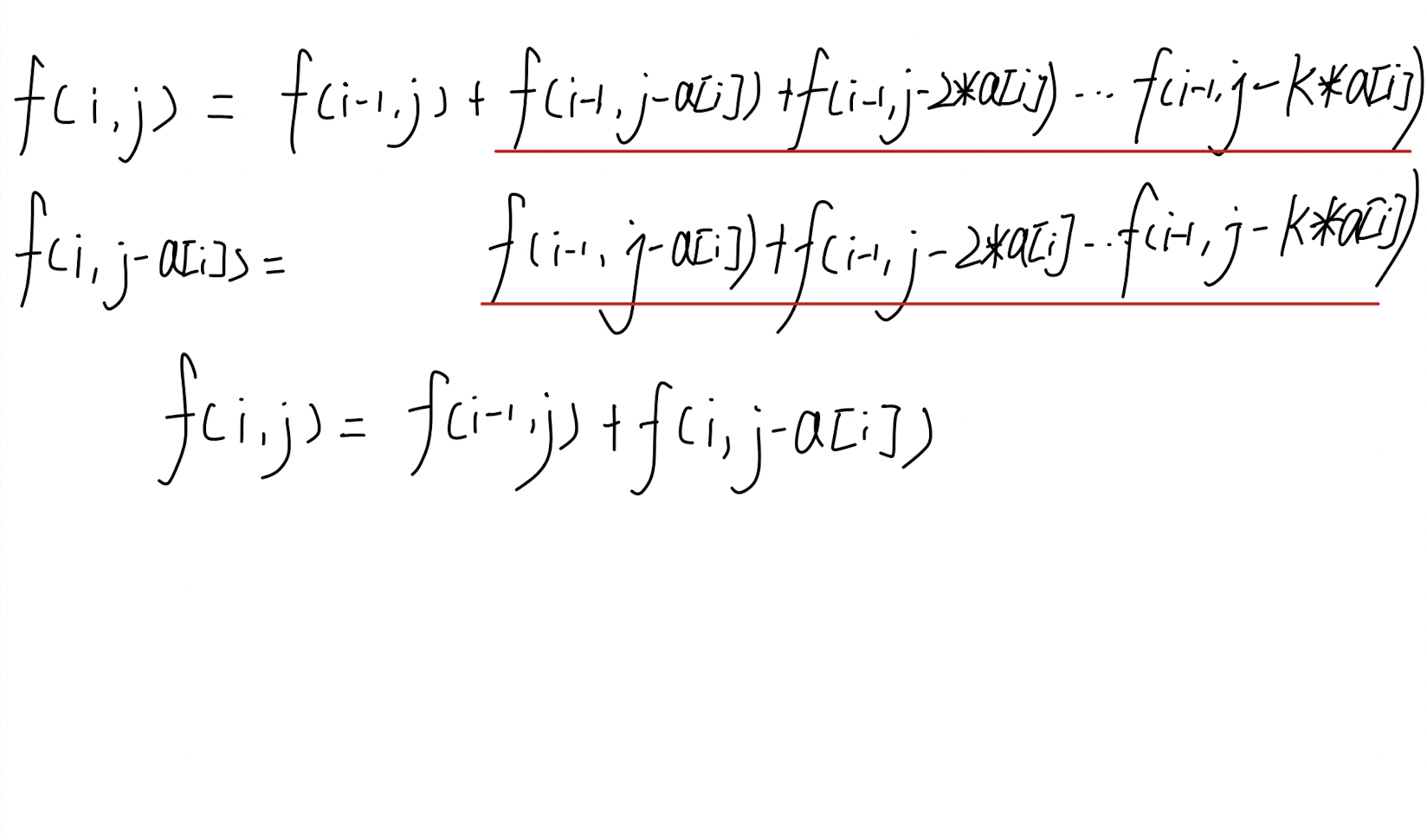
• 方程空间复杂度维度优化

f[i][j] = f[i - 1][j] + f[i][j - i] if(j >= i) (i: 1 ~ n) (j: 1 ~ n)

f[i][j] = f[i - 1][j] + f[i][j - i] (i: 1 ~ n) (j: i ~ n)

f[ j ] = f[ j ] + f[ j - i ] (i: 1 ~ n) (j: i ~ n)

f[j] 为什么是 f[i - 1][j] 而 f[j-i] 是 f[i][j-i] ?
我们在算 f[j] 的 时候 因为在这一层是 第一次 遇到 所以是上一层(i-1)的f[j]
我们在 j 这一层 遇到 j - i 由于是正序 所以 j - i 在 j 之前 被遇到过
所以 在 (j - i) 这一层之后已经被更新成了 f[i][j-i]
所以我们说在 第 j层的 f[j-i] 是 f[i][j - i];

CODE

#include<iostream>
#include<algorithm>

using namespace std;
typedef long long LL;

const LL p = 2147483648;
const LL N = 4010;

LL f[N];
LL n;

int main()
{
    cin >> n;
    f[0] = 1;

    for(LL i = 1;i < n;i ++)
    for(LL j = i;j <= n;j ++)
    f[j] =  (f[j] + f[j - i])%p;

    cout << f[n] << endl;
}