C++
\color{#cc33ff}{— > 算法基础课题解}
\color{gold}{— > 蓝桥杯辅导课题解}
思路:
二维前缀和
\color{blue}{模板}
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1]+ a[i][j]; // 求前缀和
s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);//算子矩阵的和
求二维前缀和:图解
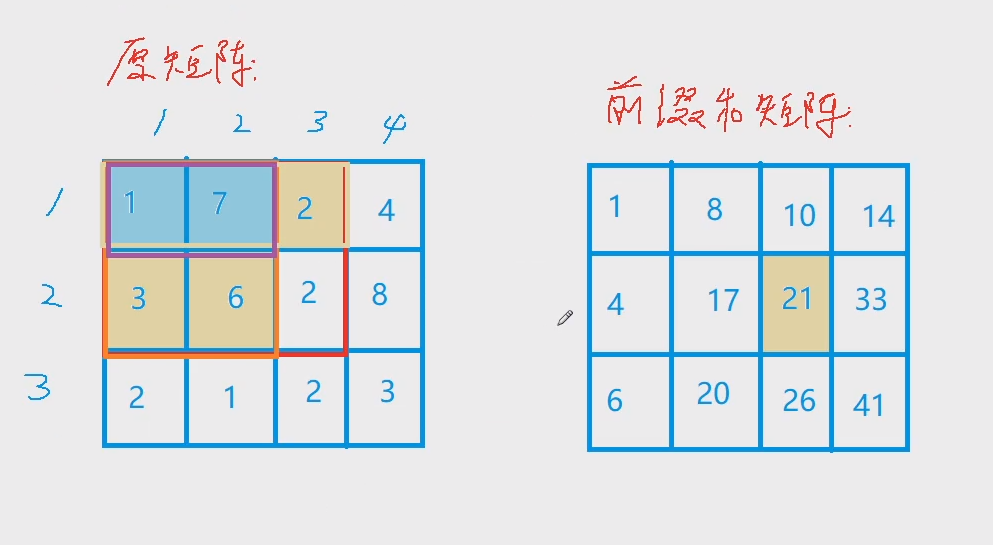
求子矩阵和:图解
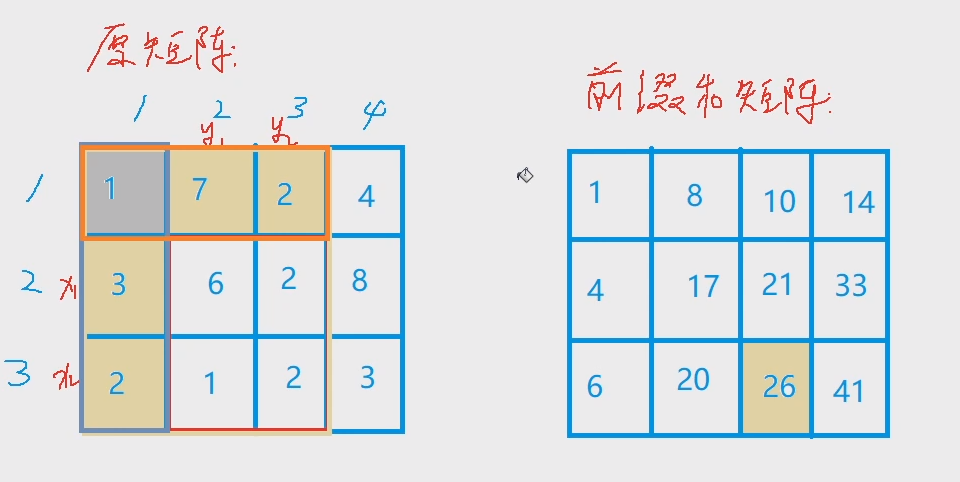
二维前缀和:

时间复杂度:O(nm)
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1e3 + 10;
int n, m, q;
int a[N][N], s[N][N];
int main() {
cin >> n >> m >> q;
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++) {
cin >> a[i][j];
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]; // 前缀和
}
while (q --) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
cout << s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 -1][y1 - 1] << endl; // 子矩阵
}
return 0;
}


orz