C++

$\color{gold}{— > 蓝桥杯辅导课题解}$

思路：

递归

$\color{#ff00ff}{图解分析：}$

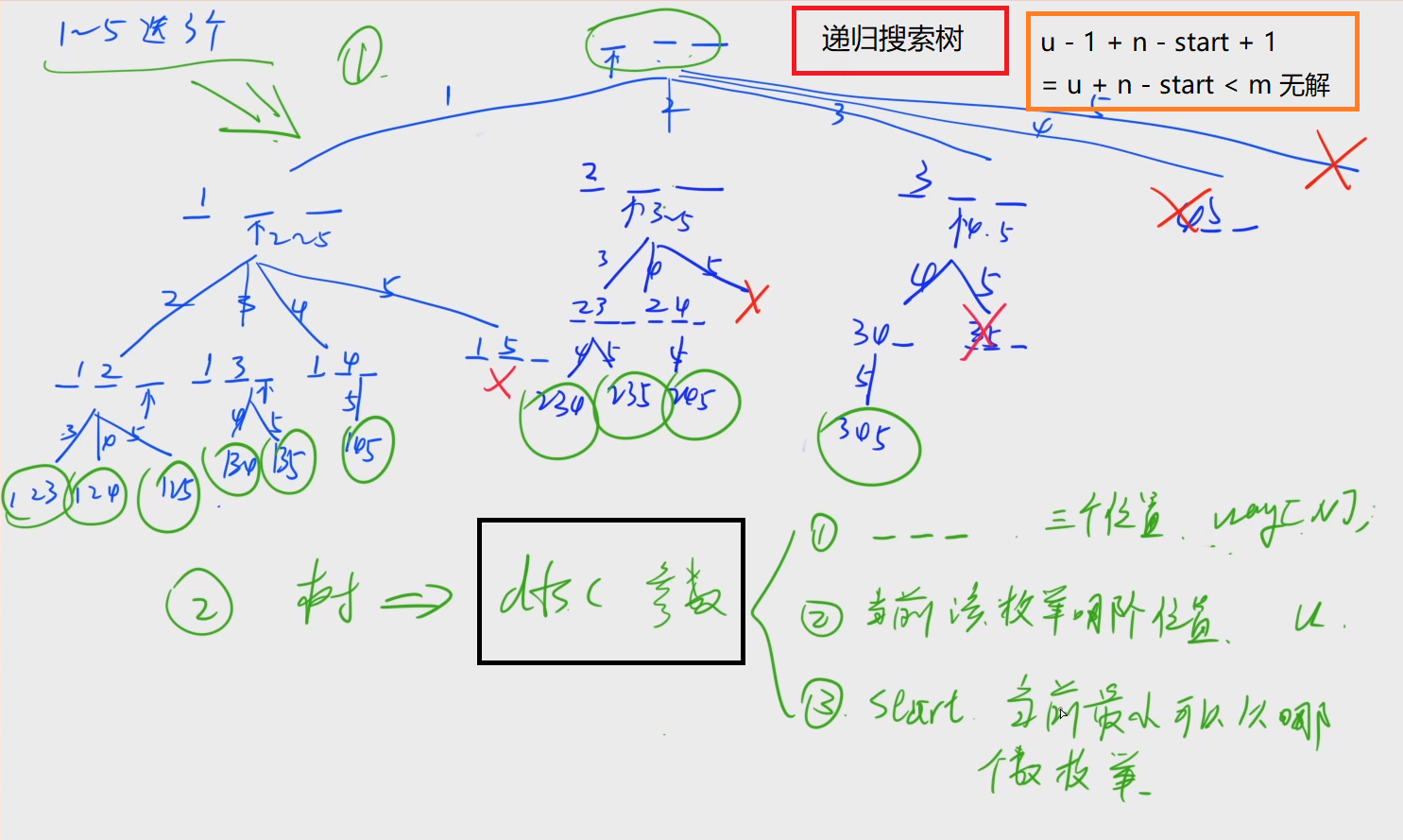
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>

using namespace std;

const int N = 30;

int n, m;
int way[N];

void dfs(int u, int start) { // u:表示当前枚举到了哪个位置，start:表示当前从哪个数开始枚举
    if (u + n - start < m) return; // 剪枝
    /*
    关于这个剪枝：
    正在选第u个数，那么表示已经选了 u-1 个数，后面是
    从 start 选到 n，如果说就算把start到n全部选上，都不够m个数的话，
    它就无解了，从start到n共n-start+1个数，如果后面可以选择的数都选上再加上
    前面已经选了的数，还是小于m的话，那么就无解了，可以return了
    整理一下：
    u - 1 + n - start + 1 = u + n - start < m，无解
    */

    if (u == m + 1) { // 到达边界 
    /*
    为什么是u == m + 1, 因为u = 1的时候，
    表示当前枚举到了第一个位置，此时还一个数都没选
    当u == m + 1时, 表示当前枚举到了第m + 1 个位置，此时已经选了m个数了
    */
        for (int i = 1; i <= m; i ++) cout << way[i] << ' ';
        cout << endl;
        return;
    }

    for (int i = start; i <= n; i ++) {
        way[u] = i;
        dfs(u + 1, i + 1);
        way[u] = 0; // 恢复现场
    }
}

int main() {
    cin >> n >> m;

    dfs(1, 1);

    return 0;
}

关于排列与组合：

$\color{blue}{排列}$：从n个不同的元素中，取r个不重复的元素，$\color{red}{按次序排列}$，称为从n个中取知r个的无重复排列。

$\color{blue}{组合}$：从n个不同的元素中，取r个不重复的元素，组成一个子集，$\color{red}{而不考虑其元素的顺序}$，称为从n个中取r个的无重组合。

$\small{分享：}$

$\large\color{blue}{— > C/C++输入字符串}$