1944 年，特种兵麦克接到国防部的命令，要求立即赶赴太平洋上的一个孤岛，营救被敌军俘虏的大兵瑞恩。

瑞恩被关押在一个迷宫里，迷宫地形复杂，但幸好麦克得到了迷宫的地形图。

迷宫的外形是一个长方形，其南北方向被划分为 $N$ 行，东西方向被划分为 $M$ 列， 于是整个迷宫被划分为 $N \times M$ 个单元。

每一个单元的位置可用一个有序数对 (单元的行号, 单元的列号) 来表示。

南北或东西方向相邻的 $2$ 个单元之间可能互通，也可能有一扇锁着的门，或者是一堵不可逾越的墙。

注意： 门可以从两个方向穿过，即可以看成一条无向边。

迷宫中有一些单元存放着钥匙，同一个单元可能存放 多把钥匙，并且所有的门被分成 $P$ 类，打开同一类的门的钥匙相同，不同类门的钥匙不同。

大兵瑞恩被关押在迷宫的东南角，即 $(N,M)$ 单元里，并已经昏迷。

迷宫只有一个入口，在西北角。

也就是说，麦克可以直接进入 $(1,1)$ 单元。

另外，麦克从一个单元移动到另一个相邻单元的时间为 $1$，拿取所在单元的钥匙的时间以及用钥匙开门的时间可忽略不计。

试设计一个算法，帮助麦克以最快的方式到达瑞恩所在单元，营救大兵瑞恩。

输入格式

第一行有三个整数,分别表示 $N,M,P$ 的值。

第二行是一个整数 $k$，表示迷宫中门和墙的总数。

接下来 $k$ 行，每行包含五个整数，$X\_{i1},Y\_{i1},X\_{i2},Y\_{i2},G\_i$：当 $G\_i \\ge 1$ 时，表示 $(X\_{i1},Y\_{i1})$ 单元与 $(X\_{i2},Y\_{i2})$ 单元之间有一扇第 $G\_i$ 类的门，当 $G\_i = 0$ 时，表示 $(X\_{i1},Y\_{i1})$ 单元与 $(X\_{i2},Y\_{i2})$ 单元之间有一面不可逾越的墙。

接下来一行，包含一个整数 $S$，表示迷宫中存放的钥匙的总数。

接下来 $S$ 行，每行包含三个整数 $X\_{i1},Y\_{i1},Q\_i$，表示 $(X\_{i1},Y\_{i1})$ 单元里存在一个能开启第 $Q\_i$ 类门的钥匙。

输出格式

输出麦克营救到大兵瑞恩的最短时间。

如果问题无解，则输出 -1。

数据范围

$|X\_{i1}-X\_{i2}|+|Y\_{i1}-Y\_{i2}|=1$,
$0 \le G\_i \le P$,
$1 \le Q\_i \le P$,
$1 \le N,M,P \le 10$,
$1 \le k \le 150$

输入样例：

4 4 9
9
1 2 1 3 2
1 2 2 2 0
2 1 2 2 0
2 1 3 1 0
2 3 3 3 0
2 4 3 4 1
3 2 3 3 0
3 3 4 3 0
4 3 4 4 0
2
2 1 2
4 2 1

输出样例：

14

样例解释：

迷宫如下所示：

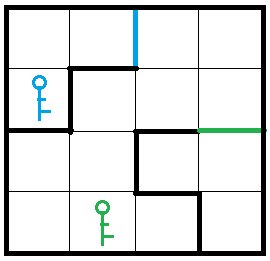
思路

注：文中把一个二维的点压成了一维，方便理解。
很明显，用一维数组$d_i$来$\text{BFS}$是肯定不行的，因为我们不知道有我们有哪些钥匙。
考虑状态压缩，把钥匙的状态进行压缩。
这里我们有两种边：

1. 捡起当前位置的钥匙，边权为$0$
2. 走向四个方向中的一个格子，边权为$1$

由于边权只有$0/1$，所以我们可以采用双端队列$\text{BFS}$。
这里说一下我对这个的理解：就是我们一开始的状态是$0$，而我们拿到一个钥匙就会回去，因为在状态的那一维是不同的，所以会走回去并且会拿着更多的钥匙。

代码

#include <iostream>
#include <deque>
#include <cstring>
#include <set>
#define x first
#define y second
using namespace std;
typedef pair <int,int> PII;
const int N = 11,M = 360,P = 1 << 10;
const int dx[] = {-1,0,1,0},dy[] = {0,1,0,-1};
int n,m,p;
int h[N * N],e[M],ne[M],w[M],idx;
int g[N][N];
int key[N * N];
int dist[N * N][P];
bool st[N * N][P];
set <PII> edges;
void add (int a,int b,int c) {
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx++;
}
int bfs () {
    memset (dist,0x3f,sizeof (dist));
    dist[1][0] = 0;
    deque <PII> q;
    q.push_back ({1,0});
    while (q.size ()) {
        auto [t,state] = q.front ();
        q.pop_front ();
        if (st[t][state]) continue;
        st[t][state] = true;
        if (t == n * m) return dist[t][state];
        if (key[t]) {
            int nstate = state | key[t];
            if (dist[t][nstate] > dist[t][state]) {
                dist[t][nstate] = dist[t][state];
                q.push_front ({t,nstate});
            }
        }
        for (int i = h[t];~i;i = ne[i]) {
            int j = e[i];
            if (w[i] && !(state >> w[i] - 1 & 1)) continue;
            if (dist[j][state] > dist[t][state] + 1) {
                dist[j][state] = dist[t][state] + 1;
                q.push_back ({j,state});
            }
        }
    }
    return -1;
}
int main () {
    cin >> n >> m >> p;
    int cnt = 0;
    for (int i = 1;i <= n;i++) {
        for (int j = 1;j <= m;j++) g[i][j] = ++cnt;
    }
    int t;
    cin >> t;
    memset (h,-1,sizeof (h));
    while (t--) {
        int x1,y1,x2,y2,c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        int a = g[x1][y1],b = g[x2][y2];
        edges.insert ({a,b}),edges.insert ({b,a});
        if (c) add (a,b,c),add (b,a,c);
    }
    for (int i = 1;i <= n;i++) {
        for (int j = 1;j <= m;j++) {
            for (int u = 0;u < 4;u++) {
                int x = i + dx[u],y = j + dy[u];
                if (x < 1 || x > n || y < 1 || y > m) continue;
                int a = g[i][j],b = g[x][y];
                if (!edges.count ({a,b})) add (a,b,0);
            }
        }
    }
    cin >> t;
    while (t--) {
        int x,y,c;
        cin >> x >> y >> c;
        key[g[x][y]] |= 1 << c - 1;
    }
    cout << bfs () << endl;
    return 0;
}