C++

$\color{#cc33ff}{— > 算法基础课题解}$

$\color{gold}{— > 蓝桥杯辅导课题解}$

思路：

整数二分(思想)：

$1、确定一个区间，使得目标值一定在区间中$
$2、找一个性质（判断条件），满足：$
$\hspace{2em}{性质具有二段性}$
$\hspace{2em}{答案是二段性的分界点}$
$3、分析终点mid在该判断条件下是否成立，$
$\hspace{2em}{如果成立，考虑答案在那个区间，}$
$\hspace{2em}{如果不成立，考虑答案在那个区间}$
$4、如果更新方式写的是r=mid,则不用做任何处理，如果更新方式写的是l=mid,则需要在计算mid时加1$

$\color{#ff00ff}{图解分析：}$

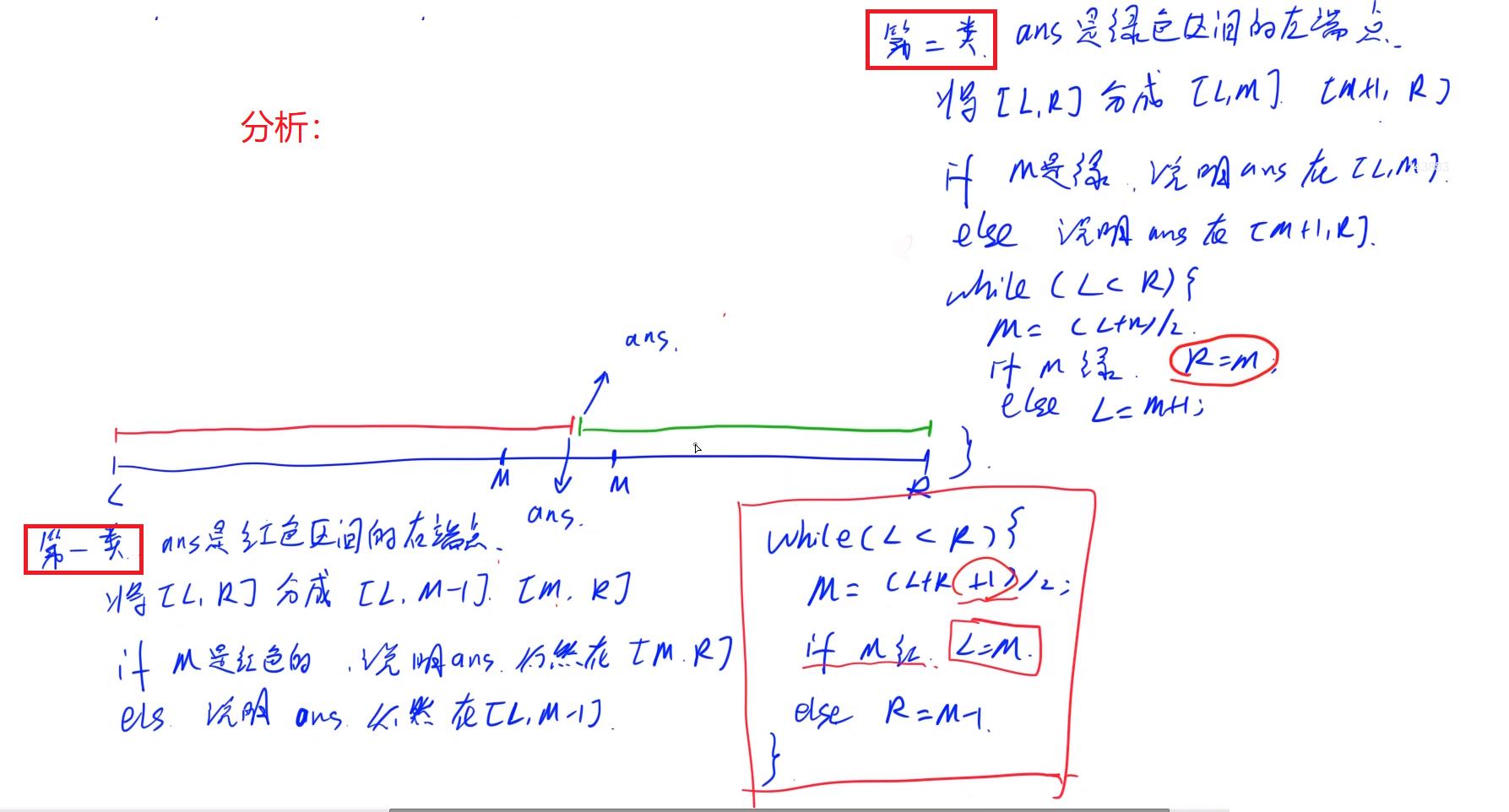
$code1:$

时间复杂度：$O(logn)$

#include <iostream>
using namespace std;

const int N = 1e5 + 10;
int n, m;
int q[N];
int main(){
    scanf("%d%d", &n, &m);

    for (int i = 0; i < n; i ++) scanf("%d", &q[i]);

    while (m -- ){
        int x;
        scanf("%d", &x);

        int l = 0, r = n - 1;
        while (l < r){
            int mid = l + r >> 1;
            if (q[mid] >= x) r = mid;
            else l = mid + 1;
        }

        if (q[l] != x) cout << "-1 -1" << endl;
        else{
            cout << l << ' ';
            int l = 0, r = n - 1;
            while (l < r){
                int mid = l + r + 1>> 1;
                if (q[mid] <= x) l = mid;
                else r = mid - 1;
            }

            cout << l << endl;
        }
    }
    return 0;
}

$code2:$

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N = 1e5 + 10;

int n, q;
int a[N];

int main() {
    cin >> n >> q;
    for (int i = 0; i < n; i ++) cin >> a[i];

    while (q --) {
        int x; cin >> x;

        // 二分x的左端点
        int l = 0, r = n - 1; // 确定区间范围
        while (l < r) {
            int mid = l + r >> 1;
            if (a[mid] >= x) r = mid;
            else l = mid + 1;
        }

        if (a[l] == x) {
            cout << l << ' ';

            // 二分x的右端点
            int r = n - 1; // 右端点一定在[左端点，n - 1]之间
            while (l < r) {
                int mid = l + r + 1 >> 1; // 因为写的是 l=mid，所以需要补上1
                if (a[mid] <= x) l = mid;
                else r = mid - 1;
            }

            cout << l << endl; // 写l和r是一样的，因为二分过后l和r是相等的
        }
        else cout << "-1 -1" << endl;
    }

    return 0;
}