算法

(大衍求一术)

对于 $A$，可以添加一条 $i \to A_i$ 的有向边，并移动图上的棋子，如果你构造出长度为 $2$ 和长度为 $3$ 的环，你就能区分出 $1 \sim 6$；如果你构造出长度分别为 $2, ~3, ~5$ 的环，你就能区分出 $1 \sim 30$。

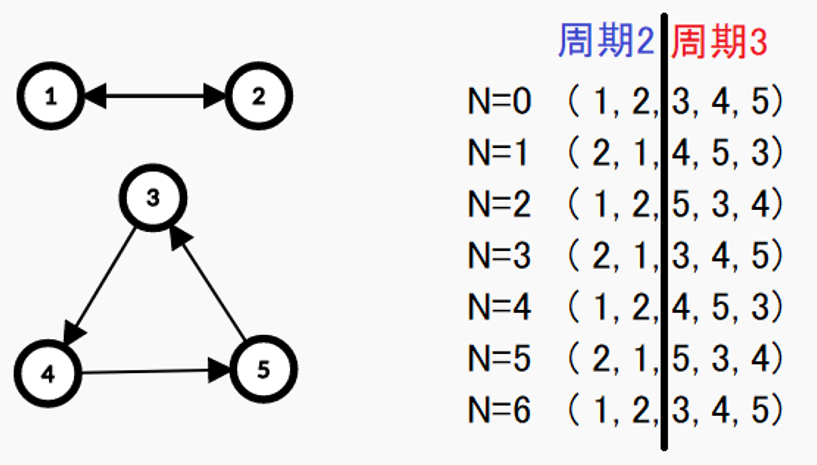
那么如何区分出 $1 \sim 10^9$ 呢？可以构造长度分别为 $2, ~3, ~5, ~7, ~11, ~13, ~17, ~19, ~23, ~29$ 的环。
但这样就有 $129$ 个点了，超过 $110$，所以不满足。

正解是构造长度分别为 $4, ~9, ~5, ~7, ~11, ~13, ~17, ~19, ~23$ 的环，总共 $108$ 个点。

C++ 代码

#include <bits/stdc++.h>
#if __has_include(<atcoder/all>)
#include <atcoder/all>
using namespace atcoder;
#endif
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

int main() {
    vector<int> ps = {4, 9, 5, 7, 11, 13, 17, 19, 23};

    vector<int> a;
    for (int p : ps) {
        int si = a.size();
        rep(i, p) a.push_back((i+1)%p+si);
    }

    int m = a.size();
    cout << m << '\n';
    rep(i, m) cout << a[i]+1 << " \n"[i == m-1];

    rep(i, m) cin >> a[i];
    rep(i, m) a[i]--;

    vector<ll> rs, ms;
    int si = 0;
    for (int p : ps) {
        rs.push_back((a[si]-si)%p);
        ms.push_back(p);
        si += p;
    }

    ll ans = crt(rs, ms).first;
    cout << ans << '\n';

    return 0;
}