宣传一下算法提高课整理 <—

本题链接（AcWing）

https://www.acwing.com/problem/content/274/

题目描述

熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。

小沐沐先让奶牛研究了最长上升子序列，再让他们研究了最长公共子序列，现在又让他们研究最长公共上升子序列了。

小沐沐说，对于两个数列 A 和 B，如果它们都包含一段位置不一定连续的数，且数值是严格递增的，那么称这一段数是两个数列的公共上升子序列，而所有的公共上升子序列中最长的就是最长公共上升子序列了。

奶牛半懂不懂，小沐沐要你来告诉奶牛什么是最长公共上升子序列。

不过，只要告诉奶牛它的长度就可以了。

数列 A 和 B 的长度均不超过 3000。

输入格式

第一行包含一个整数 N，表示数列 A，B 的长度。

第二行包含 N 个整数，表示数列 A。

第三行包含 N 个整数，表示数列 B。

输出格式

输出一个整数，表示最长公共上升子序列的长度。

数据范围

$1≤N≤3000,$序列中的数字均不超过 $2^{31}−1$。

样例输入

4
2 2 1 3
2 1 2 3

样例输出

2

思路

本题为DP问题，可以使用闫氏DP分析法解题。

DP：

我们令第一个序列为a[], 第二个序列为b[];

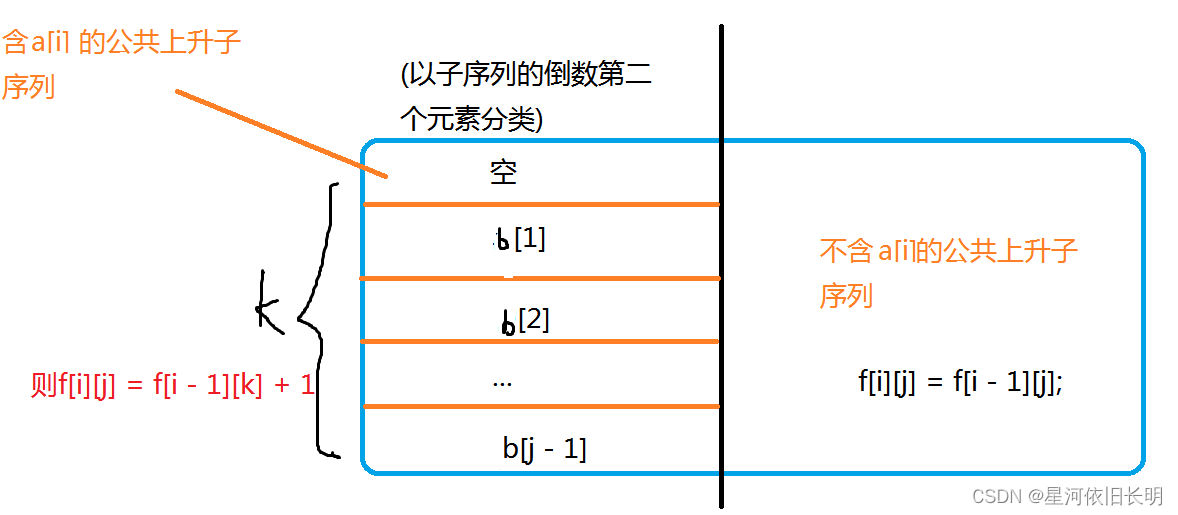
• 状态表示$f[i][j]$：
  ······集合：a的前i个数字，b的前j个数字包含的，并以b[j]结尾的所有最长公共上升子序列
  ······属性：Max
• 状态计算：
  

$TLE$ $Code$ $O(n^3)$:

$以下是C++语言朴素版代码$

#include <iostream>

using namespace std;

const int N = 3010;

int n;
int a[N], b[N];
int f[N][N];

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &b[i]);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
        {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j])
            {
                f[i][j] = max(f[i][j], 1);
                for (int k = 1; k < j; k ++ )
                    if (b[k] < b[j])
                        f[i][j] = max(f[i][j], f[i - 1][k] + 1);
            }
        }

    int res = 0;
    for (int i = 1; i <= n; i ++ )
        res = max(res, f[n][i]);

    printf("%d\n", res);

    return 0;
}

我们对此代码作适当变形，得到优化版($O(n^2)$)
$AC$ $Code$:

$C++$

#include <iostream>

using namespace std;

const int N = 3010;

int n;
int a[N], b[N];
int f[N][N];

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &b[i]);

    for (int i = 1; i <= n; i ++ )
    {
        int maxv = 1;
        for (int j = 1; j <= n; j ++ )
        {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j]) f[i][j] = max(f[i][j], maxv);
            if (b[j] < a[i]) maxv = max(maxv, f[i - 1][j] + 1);
        }
    }

    int res = 0;
    for (int i = 1; i <= n; i ++ )
        res = max(res, f[n][i]);

    printf("%d\n", res);

    return 0;
}

最后，如果觉得对您有帮助的话，点个赞再走吧！