C++
$\color{#cc33ff}{— > 算法基础课题解}$
树形dp
$图解分析:$
图一:

图二(状态计算):
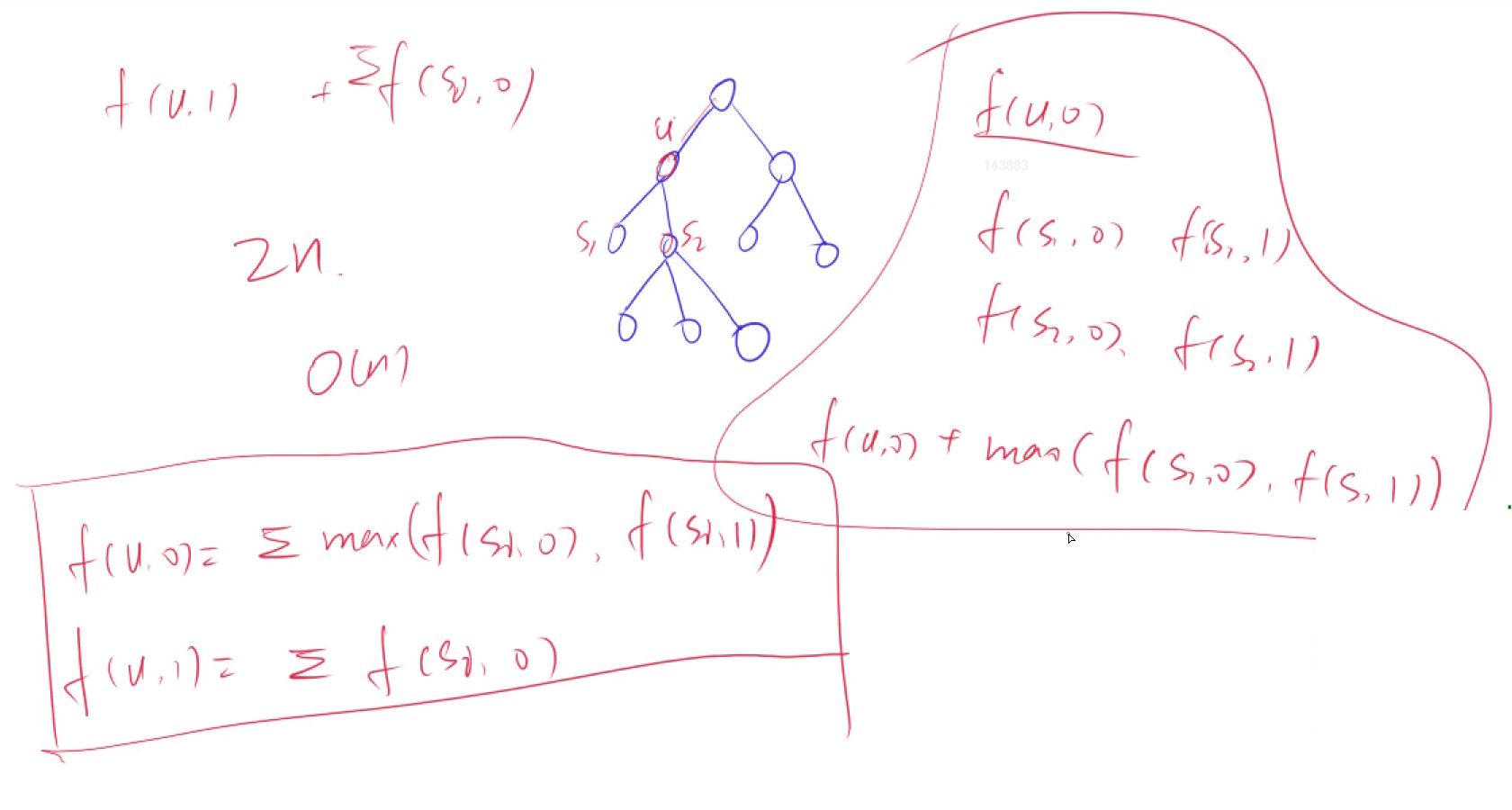
时间复杂度:$O(n)$
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 6010;
int n;
int happy[N];
int h[N], e[N], ne[N], idx;
int f[N][2];
bool has_father[N];
void add(int a, int b) { // 加边
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
int dfs(int u) { // 递归求一下每个状态
f[u][1] = happy[u]; // 选择u这个点,先加上这个点的开心度;
for (int i = h[u]; i != -1; i = ne[i]) { // 枚举u的所有儿子
int j = e[i];
dfs(j);
f[u][0] += max(f[j][0], f[j][1]); // 不选u这个点的开心度
f[u][1] += f[j][0]; // 选u这个点的开心度
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i ++) cin >> happy[i];
memset(h, -1, sizeof h); // 初始化邻接表表头
for (int i = 0; i < n - 1; i ++) {
int a, b;
cin >> a >> b;
has_father[a] = true;
add(b, a); // 由于b是a的上司,a加在b下面
}
int root = 1;
while (has_father[root]) root ++; // 确定根节点
dfs(root);
cout << max(f[root][0], f[root][1]);
return 0;
}

