AcWing 487. 超出题目本身的思考，金明的预算方案更快的解法，枚举2的N次方还是太慢了

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 487. 超出题目本身的思考，金明的预算方案更快的解法，枚举2的N次方还是太慢了原题链接中等

作者：

GensokyoLOvEr , 2020-07-15 19:39:43 , 所有人可见 , 阅读 4039

34

8

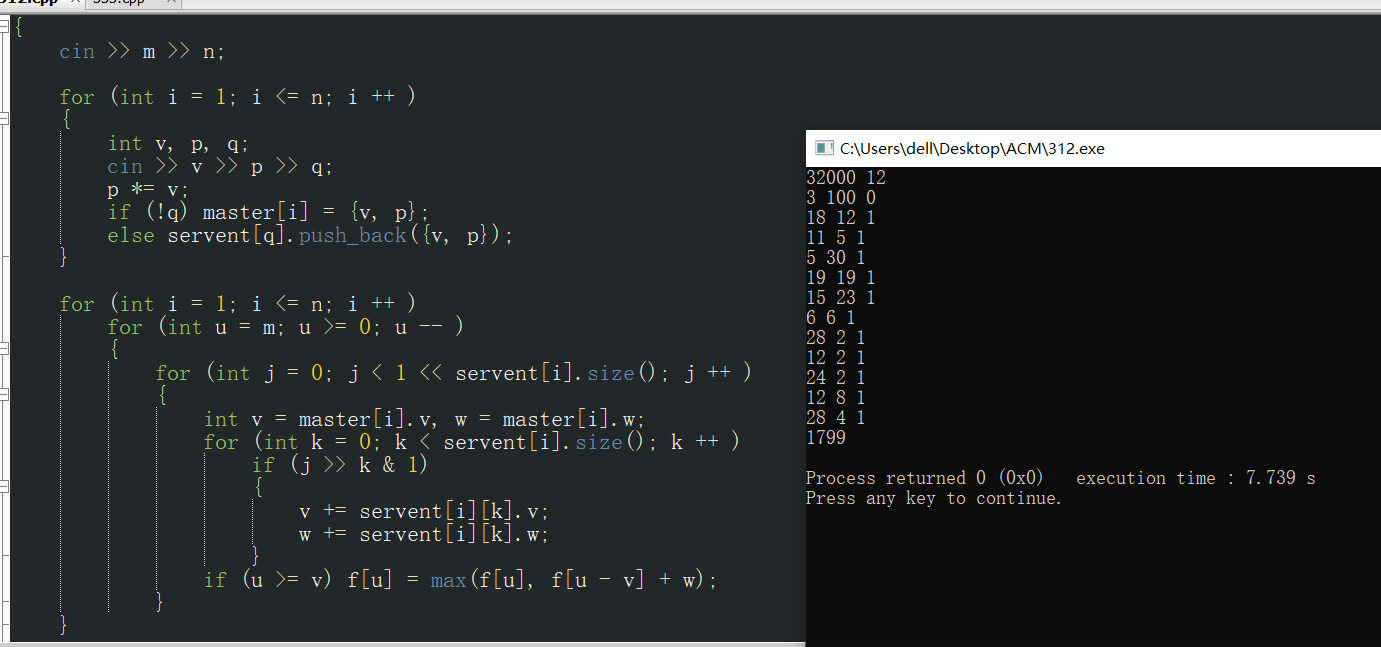
开门见山，y总对个题目的理解是将一组的电器(主件和附件)，根据条件（选附件必须选主件）进行枚举，然后利用二进制的方式去表示，假设第1个主件有M个附件，这二进制数的第i位是1则表示买第i个附件，为0则不买，从0枚举到2的M次方，这就是所有组合的情况了，但是这也很显然可以看出，如果一个主件拥有大量的附件，其实也不多比如32个(当然题目里写明了只有0，1，2个附件，所以没问题)，那么我们对一组物品的枚举数量将会大幅度提升，因为对每一个体积我们都要至少枚举4 294 967 296（2的32次方）次，这依旧在题目的数据范围内，但当我们用二进制枚举的时候已经跑不出来了，事实上当我用12个附件去测试Y总大大的代码的时候已经需要8S左右的时间了，这实在是太慢了，题目能过，但是不够快，想测试的朋友可以试一下下面这组数据
32000 12
3 100 0
18 12 1
11 5 1
5 30 1
19 19 1
15 23 1
6 6 1
28 2 1
12 2 1
24 2 1
12 8 1
28 4 1
QQ图片20200715190059.png

那好，现在我们已经知道了拖慢时间的关键在于二进制枚举，那么我们用什么办法可以来优化它呢？我们从条件入手，所有的附件的选择都只能建立在已经选择了主件的基础上，那么如果我们有一组数据里面全是选择了主件的方案，那么我们只需要对这些选择了主键的数据，用01背包的思想去枚举附件就可以了，问题在于怎么辨别哪个数据用了主键，哪个没用。而这个问题也很好解决，分步骤来就好了，当我们处理DP第I组的时候，我们先选择了第I组的主件而不选任何附件的数据进行处理，这样我们第I行DP里面凡是不为0的，就意味着选了主件，凡是为0，就意味着没选主件，然后我们就发现可以直接枚举所有的附件，比如我们枚举到第k个附件，如果dp[i][j-v[k]]!=0的时候，dp[i][j]=max(dp[i][j],dp[i],[j-v[k]]+w[k]),v[k]表示体积，w[k]表示价值,理由正如我们上面所说，第I行不为0的数据意味着选了主件，我们可以直接进行处理，如果为0就意味着没选主件，那附件也不能放上去所以跳过，这样我们每个附件只需要枚举M次而不是2的M次方次，复杂度一下子就降下来了。
再附上一组压力拉满的数据，这组数据用Y总的办法已经跑不出来了，但是我们优化后可以秒跑；
32000 60
3 100 0
18 12 1
11 5 1
5 30 1
19 19 1
15 23 1
6 6 1
28 2 1
12 2 1
3 26 1
7 28 1
25 22 1
4 3 1
23 23 1
27 22 1
6 9 1
7 18 1
19 12 1
23 10 1
20 18 1
25 26 1
22 24 1
4 3 1
15 4 1
2 22 1
29 24 1
15 18 1
28 23 1
20 28 1
22 24 1
29 20 1
6 17 1
13 21 1
17 19 1
3 11 1
29 5 1
16 27 1
10 21 1
21 11 1
22 7 1
9 4 1
24 10 1
5 25 1
21 7 1
27 17 1
29 12 1
10 25 1
14 27 1
29 18 1
13 9 1
12 10 1
6 4 1
19 20 1
1 25 1
27 28 1
7 24 1
6 12 1
23 15 1
10 1 1
20 3 1

OUTPUT
15557

样例

输入：
1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0
输出：
2200

算法代码

#include <stdio.h>
#include <cstring>
#include<stack>
#include<deque>
#include<cstdio>
#include<cmath>
#include<ctime>
#include<algorithm>
#include <iostream>
#include <queue>
#include<set>
#include <map>
#define For(i, x, y) for(int i=x;i<=y;i++)
#define _For(i, x, y) for(int i=x;i>=y;i--)
#define Mem(f,x) memset(f,x,sizeof(f))
#define Sca(x) scanf("%d", &x)
#define Sca2(x,y) scanf("%d%d",&x,&y)
#define Sca3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define Scl(x) scanf("%lld",&x)
#define Pri(x) printf("%d\n",4 x)
#define Prl(x) printf("%lld\n",x)
#define LL long long
#define ULL unsigned long long
using namespace std;
const int INF = 0x3f3f3f3f;
template<typename T> void read(T &x)
{
    x = 0;char ch = getchar();LL f = 1;
    while(!isdigit(ch)){if(ch == '-')f*=-1;ch=getchar();}
    while(isdigit(ch)){x = x*10+ch-48;ch=getchar();}x*=f;
}

int n,m;
int dp[70][42009];

struct node
{
    int v;
    int w;
};

node x[70];
node y[70][70];
int sz[70];
int a,b,c;

int main()
{
    cin>>m>>n;
    for(int i=1;i<=n;i++)
    {
        scanf("%d %d %d",&a,&b,&c);
        b=a*b;
        if(c==0)
        {
            x[i].v=a;
            x[i].w=b;

        }
        else
        {
            y[c][++sz[c]].v=a;
            y[c][sz[c]].w=b;
        }
    }

    for(int i=1;i<=n;i++)
    {
        if(x[i].v==0)//如果为0则代表这个编号是附件，在别的组里直接跳过，
        {
            for(int j=0;j<=m;j++)
                dp[i][j]=dp[i-1][j];
            continue;
        }
        for(int j=m;j>=0;j--)//优先处理只选择了主键的，然后dp[i][j]里但凡数据不是0的，都是选择了主件的；
        {
            if(j==x[i].v)
            {
                dp[i][j]=max(dp[i][j],x[i].w);
            }
            if(j>x[i].v&&dp[i-1][j-x[i].v]>0)
            {
                dp[i][j]=max(dp[i][j],dp[i-1][j-x[i].v]+x[i].w);
            }
        }
        for(int k=1;k<=sz[i];k++)//枚举所有附件，对DP[i][j-y[i][k].v](代表选择了主件)中不为0的数据进行处理
        {
            for(int j=m;j>=0;j--)
            {
                if(j-y[i][k].v>=0&&dp[i][j-y[i][k].v]>0)
                    dp[i][j]=max(dp[i][j],dp[i][j-y[i][k].v]+y[i][k].w);
            }
        }
        for(int j=0;j<=m;j++)//最后把不选主件的数据处理出来，顺序不可换，保证能识别有没有选择主键
            dp[i][j]=max(dp[i][j],dp[i-1][j]);
    }
    int res=0;

        for(int j=0;j<=m;j++)
        {
            res=max(dp[n][j],res);
        }

    cout<<res<<endl;
    return 0;
}

25 评论

Enemy 2020-10-03 11:20

把代码整理简化后加了些注释，更接近01背包，更好看一点

#include <bits/stdc++.h>
#define v first
#define w second

using namespace std;
typedef pair<int, int> PII;
const int N = 32010, M = 70;

int n, m;
PII fa[M];
vector<PII> son[M];
int f[M][N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= m; i ++ )
    {
        int a, b, c;
        cin >> a >> b >> c;
        if (!c) fa[i] = {a, a * b};
        else son[c].push_back({a, a * b});
    }

    for (int i = 1; i <= m; i ++ )
    {
        if (fa[i].v)
        {
            // 01背包，先从主件开始放
            for (int j = fa[i].v; j <= n; j ++ )
                f[i][j] = max(f[i][j], f[i - 1][j - fa[i].v] + fa[i].w);

            // 因为push_back的下标是从0开始的，遍历的时候要注意
            // 这部分判断的是，放入当前的主件，对于这个主件的附件用01背包的方式去思考求解
            // 并且当前的f[i][j]一定是已经放入当前主件的情况
            for (int k = 0; k < son[i].size(); k ++ )
                for (int j = n; j >= son[i][k].v; j -- )
                    // 放过主件以后，才能放附件，f为0的部分说明这部分放不进当前的主件
                    if (f[i][j - son[i][k].v] > 0)
                        f[i][j] = max(f[i][j], f[i][j - son[i][k].v] + son[i][k].w);
        }
        // 因为主件和附件要共同判断，但是在综合考虑之前，无法判断和前一个主件哪个更大
        // 注意i不是主件时，也要把状态传递下去
        for (int j = 0; j <= n; j ++ )
            f[i][j] = max(f[i][j], f[i - 1][j]);
    }

    cout << f[m][n] << endl;
    return 0;
}

Deep_Dark_Fantasy 2020-10-03 21:23

为什么一定是已经放入当前主件的情况呢？

Deep_Dark_Fantasy 2020-10-03 21:26

Ta有可能在另一个阶段被更新啊，所以不为零无法说明Ta是选择了主件的吧？

sdu_Lyx 2021-04-21 15:28

大佬您太强了，我的思路与您相似，但是不知道哪里出问题了

sdu_Lyx 2021-04-21 15:30

#include <bits/stdc++.h>
using namespace std;
const int N = 32110;
int m, n;
int v[N], w[N];
int ans;
vector<int> vec[N];
int vis[N];
int id;
int f[110][N];
int main()
{
    cin >> m >> n;
    for(int i = 1; i <= n; i ++ )
    {
        cin >> v[i] >> w[i];
        cin >> id;
        if(id) vec[id].push_back(i);
        else vis[i] = 1;
    }
    for(int i = 1; i <= n; i ++ )
    {
        if(vis[i])
        {
            for(int j = m; j >= 0; j -- )
            {
                f[i][j] = f[i - 1][j];
                if(j >= v[i])
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i] * v[i]);
            }
            for(auto p : vec[i])
            {
                for(int j = m; j >= v[i] + v[p]; j -- )
                {
                    f[i][j] = max(f[i][j], f[i - 1][j - v[p] - v[i]] + w[p] * v[p] + w[i] * v[i]);
                }
            }
        }
        else
        {
            for(int j = m; j >= 0; j -- ) f[i][j] = f[i - 1][j];
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

sdu_Lyx 2021-04-21 15:32

我知道了，因为这样的话漏了一种情况，谢谢大佬

cjh_0526 2021-07-20 09:30 回复了 sdu_Lyx 的评论

请问一下你这个写法会漏哪种情况

V_1 2022-05-29 08:49

再优化一下：

#include <iostream>
#include <vector>
#define v first
#define w second
using namespace std;
using PII = pair<int, int>;
const int M = 32010, N = 70;

int n, m;
PII g[N];
vector<PII> son[N];
int f[N][M];

int main() {
  scanf("%d%d", &m, &n);
  for (int i = 1; i <= n; i++) {
    int a, b, c;
    scanf("%d%d%d", &a, &b, &c);
    if (!c) g[i] = {a, a * b};
    else son[c].push_back({a, a * b});
  }

  for (int i = 1; i <= n; i++) {
    for (int j = g[i].v; j <= m; j++)
      f[i][j] = f[i - 1][j - g[i].v] + g[i].w;

    for (int k = 0; k < son[i].size(); k++)
      for (int j = m; j >= g[i].v + son[i][k].v; j--)
        f[i][j] = max(f[i][j], f[i][j - son[i][k].v] + son[i][k].w);

    for (int j = 0; j <= m; j++)
      f[i][j] = max(f[i][j], f[i - 1][j]);
  }

  printf("%d\n", f[n][m]);
}

snowys 2023-08-13 18:04

不知道还能不能优化成滚动数组，我自己尝试好像不可以

Vex 5个月前回复了 snowys 的评论

显然是可以的

#include<bits/stdc++.h>
using namespace std;
template<typename T>
inline void take_max(T &a,const T &b) noexcept
{
    if(a<b)
        a=b;
}
template<typename T>
inline void take_min(T &a,const T &b) noexcept
{
    if(a>b)
        a=b;
}
template<typename _ForwardIterator>
void print(_ForwardIterator first,_ForwardIterator last) noexcept
{
    if(first!=last)
    {
        do{
            (cout<<(*first)).put(' ');
        }while(++first!=last);
    }
    cout.put('\n');
}
typedef unsigned char uchar;
typedef unsigned short ushort;
typedef unsigned int uint;
typedef long long LL;
typedef unsigned long long ULL;
constexpr uint N=65U,M=32005U;
uint v[N],w[N],fa[N];
uint h[N],e[N],ne[N],idx;
inline void add(const uint u,const uint v) noexcept
{
    ++idx;
    e[idx]=v,ne[idx]=h[u],h[u]=idx;
}
uint dp[2U][M];
int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    // 显然是分组背包，一套主件和附件分一组
    // 一组内构成树形结构，可以树形背包，但会超时
    // 一组有n个附件的组，处理出其背包数组的时间复杂度O(n*V^2)
    // 然后背包合并，n组物品，则时间复杂度为O(n*V^2)

    // 观察数据范围
    // 本题一个主件的附件数不超过2且附件没有附件
    // 因此我们可以对一个主件的附件进行子集枚举

    // 优化
    // 如果题目只给附件没有附件，那么每一组就是一个菊花图
    // 按树形背包的思想，可以发现只要选了主件，那附件可以01背包
    // 于是就不用枚举附件的每个子集了
    // 我们在根上预留出根节点要的空间，子节点直接作为一个物品往上做01背包即可
    // 然后一组有n个附件的组，我们只用O(nV)的时间复杂度就处理出了其背包数组
    // 但处理出背包数组是需要合并的，合并复杂度不可接受
    // 考虑变换一下，把物品往总的背包数组里加
    // 先强制钦定选该组的主件，然后01背包选附件，再与不选该组的情况取max
    // 这样就变相完成了把这组物品加入背包的操作
    // 非常美妙的做法
    uint V,n;
    cin>>V>>n;
    for(uint i(1U);i<=n;++i)
    {
        cin>>v[i]>>w[i];
        w[i]*=v[i];
        cin>>fa[i];
        add(fa[i],i);
    }
    uint *cur(*dp),*last(dp[1U]);
    for(uint i(1U);i<=n;++i)
    {
        if(fa[i])
            continue;
        for(uint j(v[i]);j<=V;++j)
            cur[j]=last[j-v[i]]+w[i];
        for(uint ei(h[i]);ei;ei=ne[ei])
        {
            const uint son(e[ei]);
            for(uint j(V);j>=v[i]+v[son];--j)
                take_max(cur[j],cur[j-v[son]]+w[son]);
        }
        for(uint i(1U);i<=V;++i)
            take_max(cur[i],last[i]);
        swap(cur,last);
        // 注意到dp数组的每一个元素都是单增的，因此不用memset0
    }
    (cout<<last[V]).put('\n');
    return 0;
}

阳光男孩_7 6个月前

锟斤拷烫烫烫

Buctpeng 8个月前

大佬好强。但是这段好搞不懂：分步骤来就好了，当我们处理DP第I组的时候，我们先选择了第I组的主件而不选任何附件的数据进行处理，这样我们第I行DP里面凡是不为0的，就意味着选了主件，凡是为0，就意味着没选主件

xmkxk 2023-11-14 20:23

马蜂…

xmkxk 2023-11-14 20:24

宏定义太多了

blueecho 2022-08-12 15:57

# 妙

Thethingofenthusiasti 2022-04-26 14:56

宏定义了个寂寞

没伞的男孩 2022-01-20 21:56

请问这是DP套DP嘛

晨灼灼 2021-10-16 21:53

这种写法的思路和我的差不多，也就是类似于有依赖性背包的解法。但感觉有几处说的不太对，原句中所指的“这样我们第I行DP里面凡是不为0的，就意味着选了主件，凡是为0，就意味着没选主件，然后我们就发现可以直接枚举所有的附件”这句话个人感觉解释为“先假设放入主件，然后更新附件的值”，其实判断dp中凡是不为0的位置就相当于判断该位置是否是主件更新的范围内。也就可以用类似有依赖性背包的做法。先更新放入附件的值(0~V-v[i])(V指总钱数，v[i]指该主件的花费钱数)，然后更新放入主键的dp，在判断和原dp比较取最大值
还有就是虽然数据写的很好，但题目给的钱数要求十的倍数（可能是后来更新了题面）。建议数据可以改为10的倍数