宣传一下算法提高课整理 <—

题目描述

小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。

一次树脂拓展活动中，班上同学安排坐成一个 $m$ 行 $n$ 列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。

幸运的是，他们可以通过传纸条来进行交流。

纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标 $(1,1)$，小轩坐在矩阵的右下角，坐标 $(m,n)$。

从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。 

在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。

班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙，反之亦然。 

还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用 $0$ 表示），可以用一个 $0∼100$ 的自然数来表示，数越大表示越好心。

小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度之和最大。

现在，请你帮助小渊和小轩找到这样的两条路径。

输入格式

第一行有 $2$ 个用空格隔开的整数 $m$ 和 $n$，表示学生矩阵有 $m$ 行 $n$ 列。

接下来的 $m$ 行是一个 $m×n$ 的矩阵，矩阵中第 $i$ 行 $j$ 列的整数表示坐在第 $i$ 行 $j$ 列的学生的好心程度，每行的 $n$ 个整数之间用空格隔开。

输出格式

输出一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。

数据范围

$1≤n,m≤50$

样例输入

3 3
0 3 9
2 8 5
5 7 0

样例输出

34

思路

本题为DP问题，可以使用闫氏DP分析法解题。

从右下角回传可以等价为从左上角同时传两次，因为相当于是把路径倒过来走，最大值是不变的。
因此本题类似于1.1.3方格取数，只需将代码稍加修改即可。

考虑路径有交点的情况：

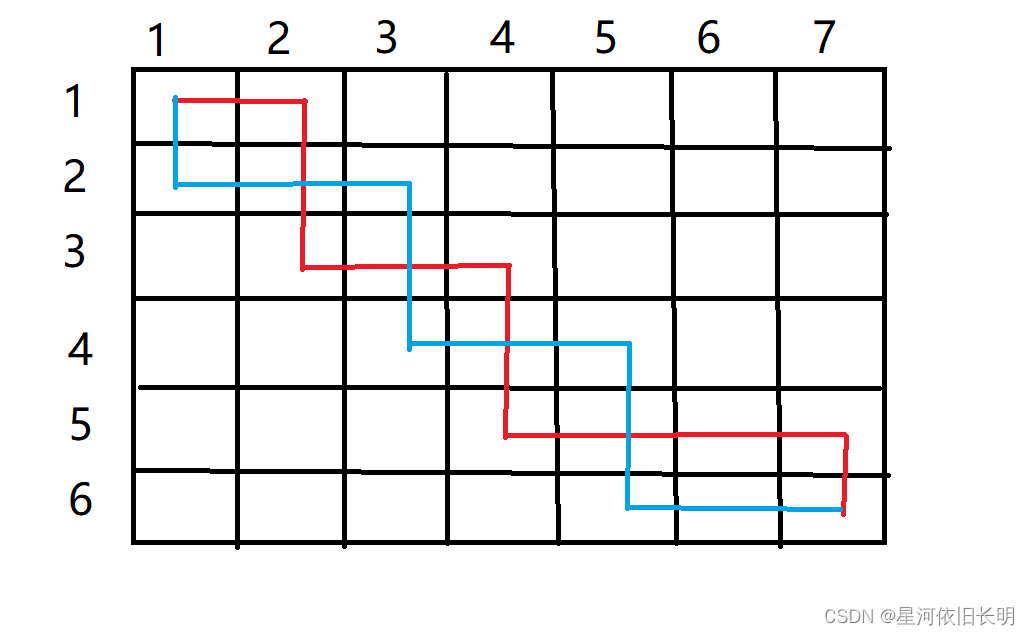
这种情况其实转换起来很简单，只要把位于红色线段上方的蓝色线段交换颜色就可以了，也就是说当红色处于蓝色的下方的时候，将红色的路径换成从蓝色的那段走是等效的（因为两条路径加起来经过的节点完全没有变）。

就可以得到：

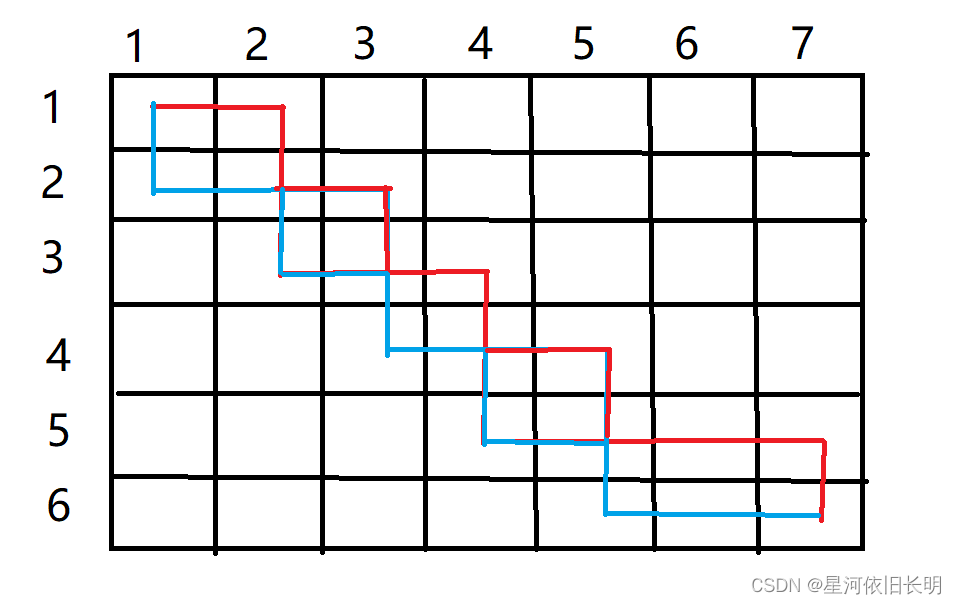
但是这个时候虽然满足了红色路径完全在蓝色的上方，但是却有交点。但是因为所有节点的权值都为非负数，那么可以证明这种情况永远不可能是最优解。比如以交点（2，2）为例，蓝色从（3，1）绕道或者红色从（1，3）处绕道一定不会比两条路径都从（2，2）处走差。

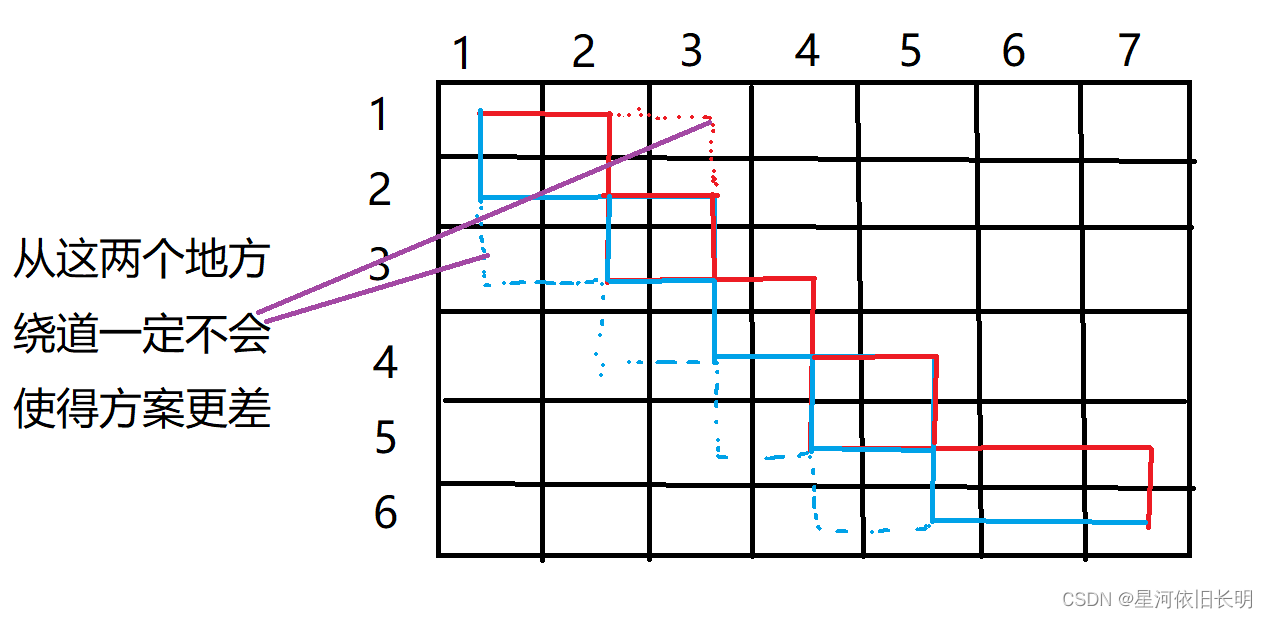
绕过交点之后，可以得到蓝色虚线的方案，该方案一定不会比之前的两个实线的方案更差。（当然该方案也不一定是最优的，还要确定应该由蓝色还是红色来走原来的交点的位置。

结论
不论是在 “方格取数” 中，还是在本题中，最优解永远不会由两段相交的路径组成。

$AC$ $Code$:

$C++$

#include <iostream>
#include <cstring>

using namespace std;

const int N = 105;

int n, m;
int w[N][N];
int f[N * 2][N][N];

int main()
{
    scanf("%d%d", &n, &m);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &w[i][j]);

    for (int k = 2; k <= n + m; k ++ )
        for (int i = 1; i < k; i ++ )
            for (int j = 1; j < k; j ++ )
            {
                int t = w[i][k - i];
                if (i != j) t += w[j][k - j];
                int &x = f[k][i][j];
                x = max(x, f[k - 1][i - 1][j - 1] + t);
                x = max(x, f[k - 1][i - 1][j] + t);
                x = max(x, f[k - 1][i][j - 1] + t);
                x = max(x, f[k - 1][i][j] + t);
            }

    printf("%d\n", f[n + m][n][n]);

    return 0;
}

最后，如果觉得对您有帮助的话，点个赞再走吧！