<—点个赞吧QwQ

宣传一下算法提高课整理

鲍勃喜欢玩电脑游戏，特别是战略游戏，但有时他找不到解决问题的方法，这让他很伤心。

现在他有以下问题。

他必须保护一座中世纪城市，这条城市的道路构成了一棵树。

每个节点上的士兵可以观察到所有和这个点相连的边。

他必须在节点上放置最少数量的士兵，以便他们可以观察到所有的边。

你能帮助他吗？

例如，下面的树：

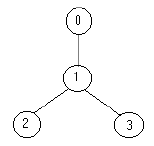
只需要放置 $1$ 名士兵（在节点 $1$ 处），就可观察到所有的边。

输入格式

输入包含多组测试数据，每组测试数据用以描述一棵树。

对于每组测试数据，第一行包含整数 $N$，表示树的节点数目。

接下来 $N$ 行，每行按如下方法描述一个节点。

节点编号：(子节点数目) 子节点 子节点 …

节点编号从 $0$ 到 $N-1$，每个节点的子节点数量均不超过 $10$，每个边在输入数据中只出现一次。

输出格式

对于每组测试数据，输出一个占据一行的结果，表示最少需要的士兵数。

数据范围

$0 < N \\le 1500$,
一个测试点所有 $N$ 相加之和不超过 $300650$。

输入样例：

4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

输出样例：

1
2

思路

这题和没有上司的舞会本质相同。
闫氏$\text{DP}$分析法：
状态表示：$f_{i,0/1}$

• 集合：在第$i$棵子树中选（$1$）或不选（$0$）根节点的最小士兵数量
• 属性：$\min$

状态计算：

• 若选了第$i$个点，那么它的子节点可以选也可以不选，即$f_{i,1}=\max\limits_{j\in son_i}\{f_{j,0},f_{j,1}\}$
• 若没有选第$i$个点，那么它的子节点一定要选，即$f_{i,0}=\max\limits_{j\in son_i}\{f_{j,1}\}$
• 所以状态转移方程是$\begin{cases}f_{i,1}=\max\limits_{j\in son_i}\{f_{j,0},f_{j,1}\}\\f_{i,0}=\max\limits_{j\in son_i}\{f_{j,1}\}\end{cases}$

初始状态：$f_{i,0}=0,f_{i,1}=1(i\in [1,n])$
目标状态：$\max\{f_{1,0},f_{1,1}\}$
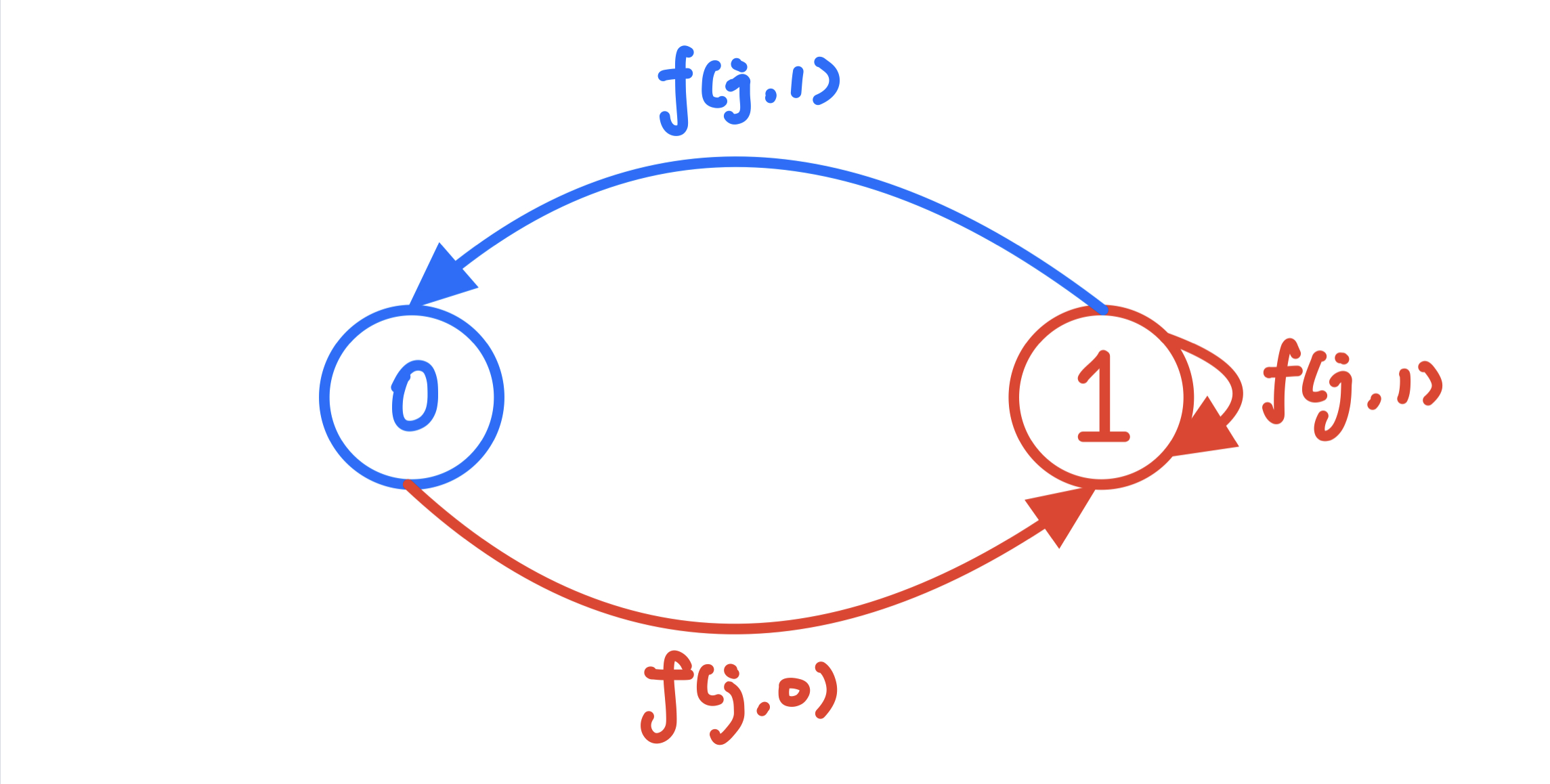
来自一只野生彩色铅笔的状态机模型：

代码

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1510,M = 2 * N;
int n;
int h[N],e[M],ne[M],idx;
int f[N][2];
void add (int a,int b) {
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}
void DP (int u,int fa) {
    f[u][0] = 0,f[u][1] = 1;
    for (int i = h[u];~i;i = ne[i]) {
        int j = e[i];
        if (j == fa) continue;
        DP (j,u);
        f[u][1] += min (f[j][0],f[j][1]);
        f[u][0] += f[j][1];
    }
}
int main () {
    while (cin >> n) {
        memset (h,-1,sizeof (h));
        idx = 0;
        for (int i = 1;i <= n;i++) {
            int x,k;
            char ch;
            cin >> x >> ch >> ch >> k >> ch;
            x++;
            while (k--) {
                int y;
                cin >> y;
                add (x,++y),add (y,x);
            }
        }
        DP (1,0);
        cout << min (f[1][0],f[1][1]) << endl;
    }
    return 0;
}