$\LARGE\color{orange}{刷题日记(算法提高课)}$

我们从样例的角度来考虑这个问题

上面为样例，下面为最长上升子序列的长度

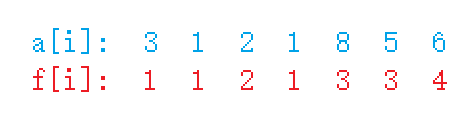
我们设 $len$ 表示上升子序列的长度，我们考虑 $len\ =\ 1$ 的情况

当上升子序列的长度为 1 时，结尾的数的选择有两个：1 和 3 ，这时我们考虑，选哪个更好

注意到 $a[2]\ =\ 2$ ，因此如果我们选择 3 的话，那么 $f[2]$ 只能为 1 ，但如果我们选择 1 的话， $f[2]$ 就可以为 2

也就是说，当上升子序列的长度固定时，结尾的数越小越好，这样我们便有更大的可能性得到一个更长的上升子序列

我们用 $q[i]$ 表示当上升子序列长度为 $i$ 时所对应的数为 $q[i]$ ，我们设定初始的最长上升子序列长度 $len$ 为 0

每当我们变遍历到一个新数 $a[i]$ 时，我们动态调整 $q[i]$ 数组

找到 $q[i]$ 当中第一个严格小于 $a[i]$ 的数（设其下标为 $idx$），之后我们更新 $q[idx]$ 与 $len$

最后的 $len$ 便是最长上升子序列的长度

完整代码：

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int a[N], q[N];//q[i]表示长度为i的上升子序列的结尾数字
int n;

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++)
        cin >> a[i];
    int len = 0;
    q[0] = -1e9;//避免出界
    for(int i = 1; i <= n; i++)
    {
        int l = 0, r = len;
        while(l < r)//二分，找到q[i]中第一个比a[i]小的数
        {
            int mid = l + r + 1 >> 1;
            if(q[mid] < a[i]) l = mid;
            else r = mid - 1;
        }
        q[l + 1] = a[i];//对q[i]和len进行更新
        len = max(len, l + 1);
    }
    cout << len << endl;
    return 0;
}