$\LARGE\color{orange}{刷题日记(算法提高课)}$

这道题看上去跟 AcWing 1027. 方格取数 类似，我们考虑能不能将其转换过去

首先，从 $(n,\ m)$ 走到 $(1,\ 1)$ 等价于从 $(1,\ 1)$ 走到 $(n,\ m)$ ，因此这道题也可以看成是从 $(1,\ 1)$ 走两次到 $(n,\ m)$ 并取路径和的最大值

再者，方格取数那道题中，是允许两条路线相交的，本题是不允许这一点的

但由于我们需要找的是最优路线（路径和最大），因此只要我们能过证明路径和最大的两条路线没有交点，那么这道题就可以完全等价到方格取数那道题

下面我们给出证明：

对于任意一种路线交叉的情况，我们都可以将其变为一条路线在上另一条路线在下的一般情况

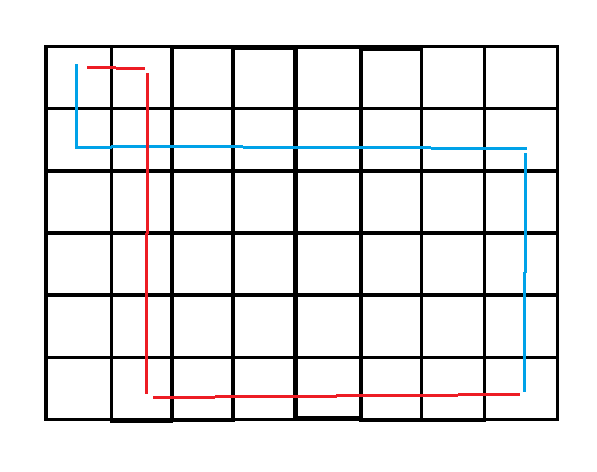
可以变为

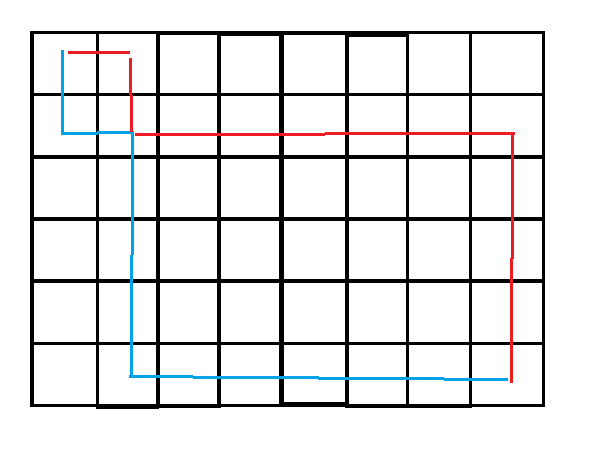
在方格取数当中，路线交叉位置的格子当中的数只能取一次，并且所有格子的权重均为非负数

因此我们便可以在交叉位置处对路线进行微调，进而构造出一个路径和更大的解

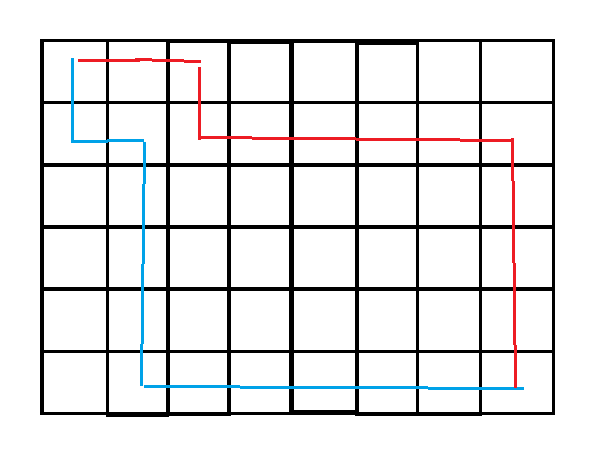
也就是说，对于任意两条相交路径，一定存在两条不相交路径使得后者路径和大于前者

因此，最优解的两条路径一定不可能重合

也就是说，本题可以直接使用方格取数的代码

这里我们对代码进行一些补充说明：

• $k$ 的定义为当前所走的步数，即横纵坐标和的最大值

• 原代码中可以省略掉对 $j$ 的判断，我们需要保证 $max(1,\ k\ -\ m)\ \le\ i1 \ \le\ min(n,\ k\ -\ 1)$

由于 $j1\ =\ k\ -\ i1$ 且 $1\ \le\ j1\ \le\ m,\ 1\ \le\ i1\ \le\ n$

不难得出 $1\ \le i1\ \le\ k\ -\ 1,\ k\ -\ m\ \le\ i1\ \le\ n$

左边取最大值，右边取最小值，有：$max(1,\ k\ -\ m)\ \le\ i1 \ \le\ min(n,\ k\ -\ 1)$

代码如下：

#include <iostream>

using namespace std;

const int N = 55;

int f[N * 2][N][N], w[N][N];

int n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            cin >> w[i][j];

    for(int k = 2; k <= n + m; k++)
        for(int i1 = max(1, k - m); i1 <= min(n, k - 1); i1++)
            for(int i2 = max(1, k - m); i2 <= min(n, k - 1); i2++)
                {
                    int j1 = k - i1, j2 = k - i2;
                    int t = w[i1][j1];
                    if(i1 != i2) t += w[i2][j2];
                    for(int a = 0; a <= 1; a++)
                        for(int b = 0; b <= 1; b++)
                            f[k][i1][i2] = max(f[k][i1][i2], f[k - 1][i1 - a][i2 - b] + t);
                }
    cout << f[n + m][n][n] << endl;
    return 0;
}