核心代码
int find(int x)
{
if(p[x] != x)
{
int tmp = find(p[x]);
d[x] += d[p[x]];
p[x] = tmp;
}
return p[x];
}
注意事项,即明白 d[i] 的含义
看了几位同学分享的代码还有题解,对于d[i]的理解其实是有误的,d[i]的正确理解,应是第 i 个节点到其父节点距离,而不是像有些同学所讲的,到根节点的距离!!这点大家一定要搞清楚,之所以有这样的误会,是因为find()函数进行了路径压缩,当查询某个节点 i 时,如果 i 的父节点不为根节点的话,就会进行递归调用,将 i 节点沿途路径上所有节点均指向父节点,此时的 d[i] 存放的是 i 到父节点,也就是根节点的距离。
下面为了更好的理解函数调用过程以及d[i]的变化,我将插图分享给大家
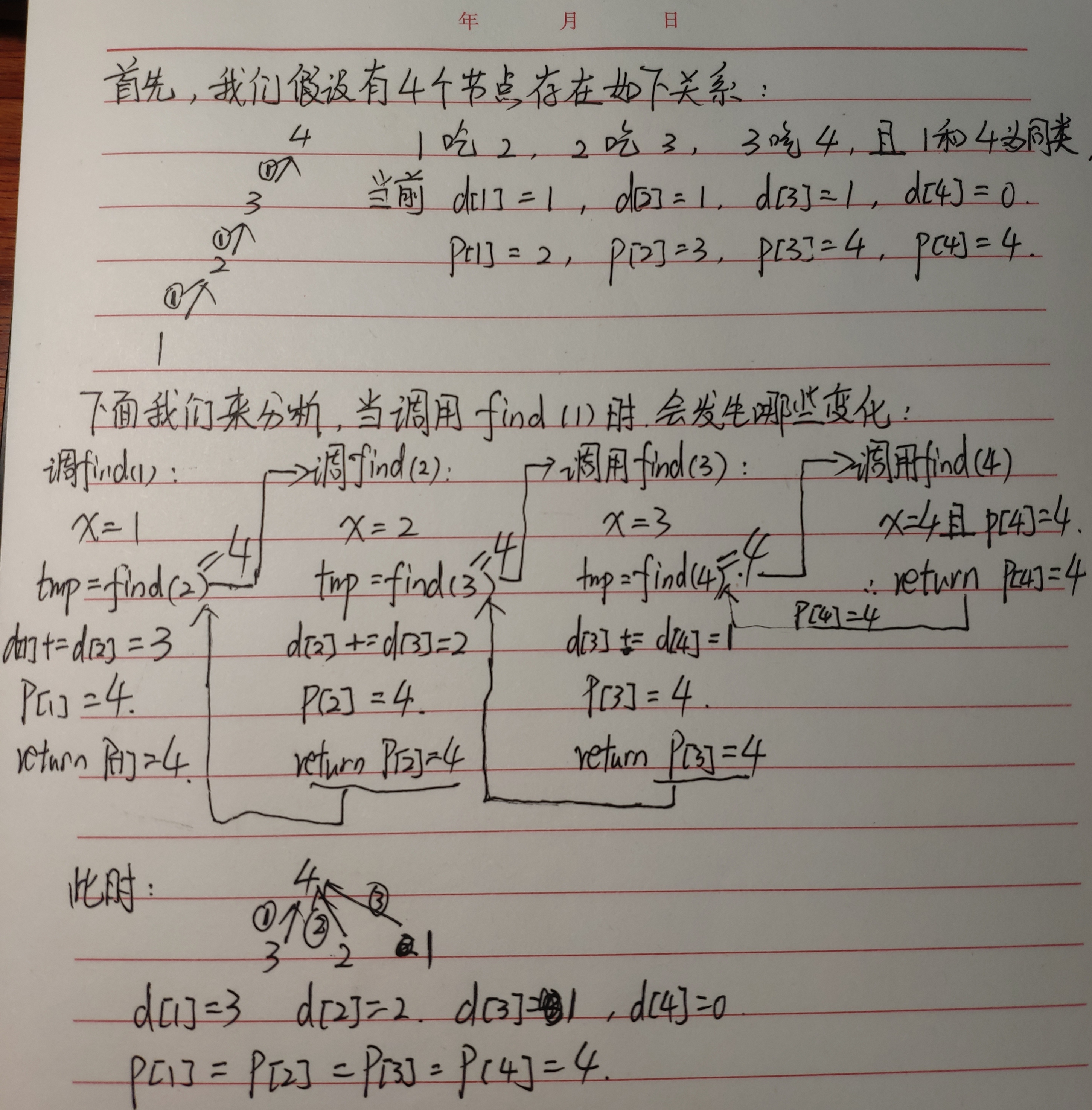
以上是我针对此题过程的理解,如有不对的地方,还望大家指出,谢谢!


确实清楚,每次递归模拟我都要模拟好久,感谢┗|`O′|┛ 嗷~~
┗|`O′|┛ 嗷~~
┗|`O′|┛ 嗷~~ 递归会一直在我的脑子里走一遍才行
┗|`O′|┛ 嗷~~
确实在所有情况下都是到父节点的距离,没更新的时候也是。只不过你每次要取得d[x]的时候,他都必然会经过一次更新的过程(执行find(x)),因此每次取得d[x]其实也是到根结点的距离。除非你不find更新直接取d[x]。
总结一下:不路径压缩取得的是到父节点的距离,路径压缩后既是到根的距离,也是到父节点的距离,因为压缩后将父亲指向根了,父亲和根是一个东西。而由于每次取d[x]都必然经过路径压缩,因此d[x]在结果上既是到根的距离,也是到父亲的距离。但是在过程中它仅代表到父亲的距离,因为没更新的时候它的父亲并不是根。
和
这两个的区别在哪,为什么一定要一个t来存储才行呀
find函数不仅负责找到根节点,也负责递归计算d[x],因此你上下调换一下虽然看起来对,实际上并没有将d[p[x]]的最终值计算出来,所以在d[x]的计算上会出问题。
懂了懂了,orz
但是他状态压缩完只有两层啊,递归也最多两层,旧父亲到根的的距离已知的啊
未知的,d[p[x]]是旧父亲到旧父亲的旧父亲的距离,旧父亲的旧父亲不一定是根,压缩完了才是。
懂了!!!谢谢大佬orz
路径压缩完,他也就只有一个父节点,就是它的祖宗节点
请问下这样写为啥是错的呀
你这样的,是先从深到浅加d[]数组,再递归往回。d[x] += d[p[x]]是加在靠深位置的d[]数组上,往回走的时候无法起到累加的作用,最终应该会导致除了根节点其他d[]都是2。而在正确的顺序下,是在递归过后往回递推的时候才会进行累加,从浅到深,加在靠深的位置,这样才能起到累加的作用。
要调用find()函数
模拟一下就会发现,d[x]+=d[p[x]]是加的p[x]到它自身父节点的距离,而答案求的是加上p[x]到根节点的距离。所以应该先递归求出p[x]到根节点的距离,再回溯更新d[x]
非常清楚
因为int t = find(p[x])这个语句是为了进行路径压缩的,要使得同一个集合里面所有元素对应p数组的值一样,这样t的值就是根结点的值,再让p[x] = t。先从叶子递归到根节点,再从根节点逐渐返回,传递根节点的值。
如果你这样写,会影响第d数组,因为先执行路径压缩才会导致x的父节点指向根节点,然后此时x到父节点的距离加上父节点到根节点的距离才是x到根节点的距离,然后再让x的父节点为根节点。如果你注释掉,x的父节点指向的就不是根节点,那么这个d[x] += d[p[x]];算出来的也是错的。
此代码中,路径压缩前,
d[x]存放的是真正的结点x到底根节点p[x]的距离,但是路径压缩后,d[x]的距离就不再有意义。因为路径压缩后,x的父节点1变成了原集合的根节点,而d[x]存放的是路径压缩前到达父节点的集合,所以路径压缩后父节点发生改变,d[x]也就毫无意义。2024.11.7,晚上11:00,真爱死你了bb
楼主画图讲解递归的过程确实很棒,但是关于d[i]的理解我不敢苟同。
d[i]的正确定义肯定是i到根节点的距离,因为同一个并查集中只有根节点是唯一的,只有计算所有节点到根节点的距离才能正确刻画节点之间的关系。虽然路径压缩使得根节点成为了所有节点的父节点,但是路径压缩是原树的等价变换,本质上还是到根节点的距离。
第一次确定的d[i]是到父节点距离,find之后的d[i]是到树根的距离这样
一开始是到父节点距离,递归调用完才因为路径压缩了才是到根节点距离
萌新疑惑一波:find()里的d[x]+=d[p[x]];
如果是到根节点的距离,“归”时的累加,d[x]=一个个到根节点距离的累加,不会导致d[x]的错误吗?
而如果按照到父节点的距离理解,d[x]=一个个到父节点距离的累加,似乎合理一点。
呵呵了您呐
这个其实只执行了一次阿。
你还反对上了,d[i]在没有执行路径压缩的时候就不是到根节点的距离,你后半段话都是废话。
因为执行完路径压缩后,x的所有祖宗都指向了根节点,所以d[p[x]]就是x的父节点到根节点的距离,而此时x没有指向根节点!!!!!!!(记住这句话),所以d[x]的值是x到父节点的距离,两者相加就是x到根节点的距离,之后再执行p[x] = u,让x执行根节点。
你好,大佬,我可以这样理解吗,其实就是我一直递归到当前节点的祖先节点,然后再从祖先节点一直往下,累加他的值,这也正好就是递归的回溯过程,但是在这个过程中,我会将路径上的所有节点的父节点也修改为祖宗节点(即所谓的路径压缩):
可以这样理解
int tmp = find(p[x]);
d[x] += d[p[x]];
p[x] = tmp;
因为执行完路径压缩后,x的所有祖宗都指向了根节点,所以d[p[x]]就是x的父节点到根节点的距离,而此时x没有指向根节点!!!!!!!(记住这句话),所以d[x]的值是x到父节点的距离,两者相加就是x到根节点的距离,之后再执行p[x] = tmp,让x指向根节点。
我这段话完整阐述了这三行代码的作用,明白的给我点个赞吧hh
姐妹牛逼!!! 距离更新实在路径压缩之前更新的,所以d[x]代表的是x到其父节点的距离
爱了爱了,一下子对递归有了理解💎 💎
d不都是0吗,怎么维护
我也想不明白这点,d数组所有的初始值都是0,为啥一开始就是d[1]=1,d[2]=1,d[3]=1,d[4]=0
初始化的时候d是0,后面画1,2,3,4关系的时候,进行合并操作,合并函数中对d进行操作,d[i]第 i 个节点到其父节点距离,也就是没有进行路径压缩的之前,比如 d[1] = 1到2的距离
后面进行合并操作改变的d[i],这里能再分析一下吗?确实不太理解为什么一上来d[i]就有值。
我也想知道这个d[i]怎么改变的
在main函数中,判断a吃b的关系里,若a和b属于不同的集合,要合并,并且距离+1,因此d就被赋值了
只要存在相吃的关系,
d[px] = d[y] + 1 - d[x];就会更新d[px]距离,从而该集合上的dx就会进行变化。可是代码运行顺序是先find(),再d[px] = d[y] + 1 - d[x];
并查集中不是说一个节点到他的父节点的距离就是1, 这个距离是由这两个点的关系来定的
x, y是同类的话的
d[x]与d[y]模三同余(路径压缩后根节点就是父节点)x吃y的话的
d[x] - 1与d[y]模三同余y吃x的话的
d[x] + 1与d[y]模三同余赞
orz
还是有点难理解😭find函数
递归过程想明白了 就很简单
d[1] = 1, d[2] = 1, 你d[1] += d[2] 等于3是吧
在回溯过程中d[2] += d[3],此时d[2]就成了2。
肯定请水军了,这题解狗都不看
?说话这么戾气
你的头像也是挺抽象的呵
还行吧,但素质还在呢
恶语相向就不好了朋友,觉得题解写的不好,愿意给建议就给,不愿意给也不要丢了您的素质,最起码人家是无偿分享。
看了你的空间,一个题解分享都没有,就不要说别人了
好的,不好意思。
你可能没有看懂,但是这个题解真的帮了我很大的忙
# $\Huge{stOOrz}$
orz
递归到底是啥意思
借个图大佬
能不能这样理解 路径压缩前的d[x]是x到父结点p[x]的距离 路径压缩后 p[x]递归调用后指向根结点 在此过程中 d[u]也递归调用是旧的p[x]到根结点的距离 递归调用后 x也要指向根结点 所以是旧d[x]+d[u]
感谢感谢,学到了,以后可以在纸上模拟递归的过程了
压缩前是父节点,压缩后是根节点
这个不是很理解,不是求 d [ x ] 或者 d [ y ] 到节点 0 的距离吗?为什么是求 d [ px ]呢?