$\Huge\color{orchid}{点击此处获取更多干货}$

两个栈

输入表达式后先在末尾加上#（结束符）
用一个操作数栈opnd和一个操作符栈oprt，进出栈操作有以下规则：
1、遇到操作数，取得所有数位后合成数字，直接进opnd栈
2、遇到操作符，需要和oprt栈顶的操作符比较优先级，如果目前操作符优先级较高，就让当前字符进入oprt栈，如果优先级较低则按顺序取出操作数2，操作符和操作数1，计算得到结果继续进opnd栈
3、如果当前是右括号但栈顶是左括号，直接让左括号出oprt栈，然后什么都不用做直接读取下一个字符
4、当前字符为#时可以直接结束，因为此时oprt栈顶必然是#（保证输入合法）

下面展示操作符优先级表：

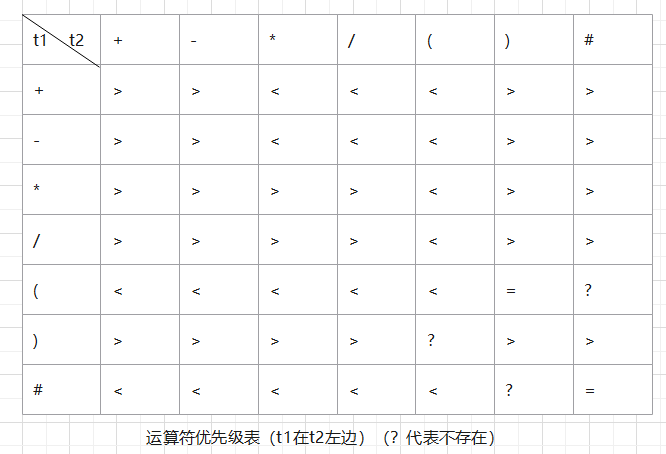
同级运算符从左到右，乘除高于加减
左括号可以直接进栈，右括号优先级仅仅比结束符高，因此可以直接出两数一符（如果有数的话）

可以发现，上述的操作数栈opnd是个普通栈，而从优先级来看，操作符栈oprt是个单调减少的栈
详情请见注释

C++ 代码

#include <iostream>
#include <string>
#include <stack>
using namespace std;

char Precede(char c1, char c2)//从左到右先乘除后加减，遇到左括号直接进栈，遇到右括号直接出2数1符计算
{
    if ((c1 == '+' || c1 == '-') && (c2 == '+' || c2 == '-' || c2 == ')' || c2 == '#'))
    {
        return '>';
    }
    else if ((c1 == '*' || c1 == '/' || c1 == ')') && (c2 != '('))
    {
        return '>';
    }
    else if (c1 == '(' && c2 == ')')
    {
        return '=';
    }
    else
    {
        return '<';
    }
}

int Calculate(int a, char t, int b)
{
    int ans = 0;
    switch (t)
    {
    case '+':
    {
        ans = a + b;
        break;
    }
    case '-':
    {
        ans = a - b;
        break;
    }
    case '*':
    {
        ans = a * b;
        break;
    }
    case '/':
    {
        ans = a / b;
        break;
    }
    }
    return ans;
}

int main()
{
    stack<int> opnd;
    stack<char> oprt;
    string expression;
    cin >> expression;
    expression += '#';//结束符
    oprt.push('#');
    int len = expression.size();
    int i = 0;
    while (expression[i] != '#' || oprt.top() != '#')
    {
        char ch = expression[i];
        if (isdigit(ch))
        {
            int j = i, op = 0;
            //数字位数可能不止一位
            while (j < len && isdigit(expression[j]))
            {
                op = op * 10 + expression[j++] - '0';
            }
            opnd.push(op);//转化为数之后进opnd栈
            i = j;
            //顺便指出，之前置顶的题解Hasity写的有问题，i = j - 1之后还是会回到数字上，造成MLE和死循环
        }
        else
        {
            switch (Precede(oprt.top(), ch))
            {
            case '<'://当前字符进oprt栈
            {
                oprt.push(ch);
                i++;
                break;
            }
            case '>'://出两数一符，计算结果进opnd栈
            {
                int a = opnd.top();
                opnd.pop();
                int b = opnd.top();
                opnd.pop();
                char t = oprt.top();
                oprt.pop();
                opnd.push(Calculate(b, t, a));
                /*
                * 关于Calculate的传参顺序：
                * 出栈的顺序是a,b，传参的顺序一定是b,a 
                * 加法和乘法交换操作数顺序没关系
                * 减法和除法会出问题
                * b/a的时候先入第一个操作数b再入第二个操作数a
                * 但出栈的时候操作数2(a)会比操作数1(b)先出栈
                * 此时如果写Calculate(a,t,b)就会导致错误结果，一定是Calculate(b,t,a)
                */
                break;
            }
            case '='://括号匹配出栈
            {
                oprt.pop();
                i++;
                break;
            }
            }
        }
    }
    cout << opnd.top() << endl;
    return 0;
}