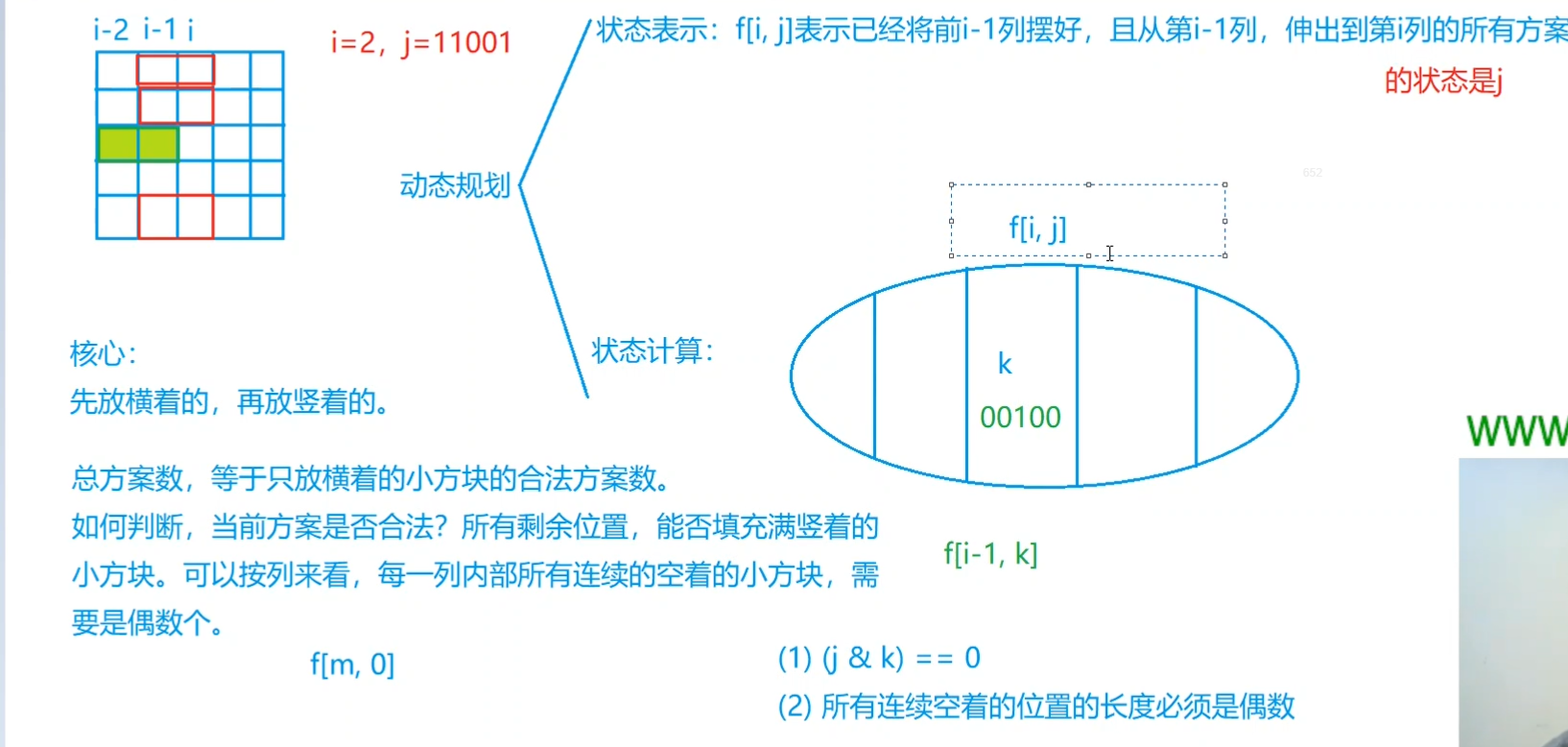
核心：

摆放的小方格方案数 等价于 横着摆放的小方格方案数

如何判断当前方案是否合法？

遍历每一列，i列的方案数只和i-1列有关系

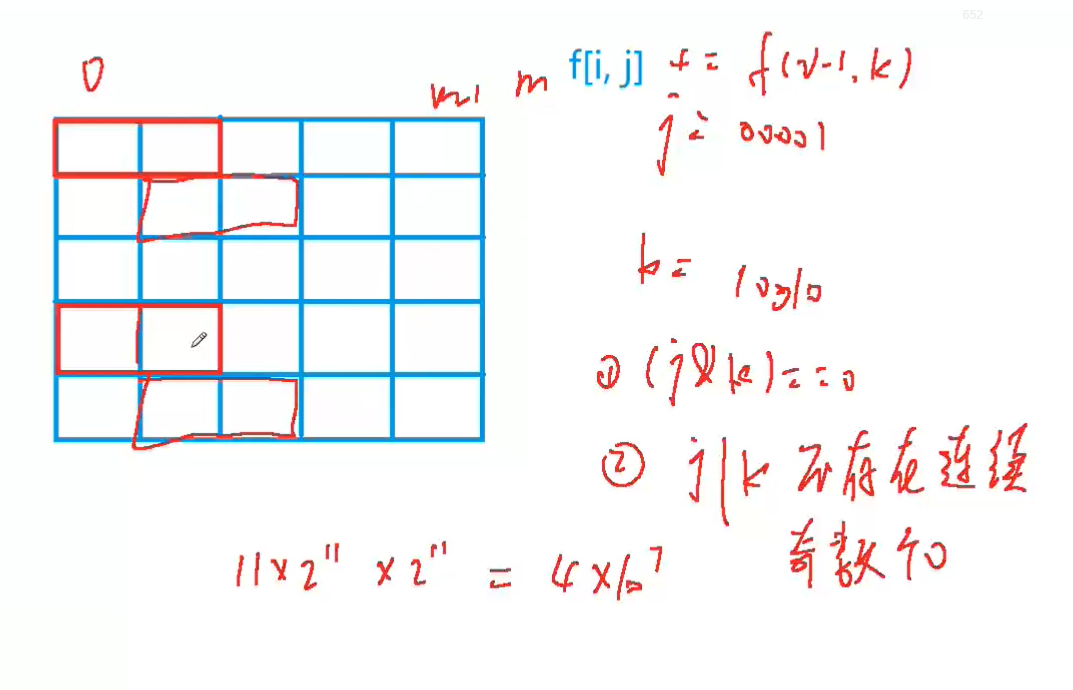
• j&k==0， i-2列伸到i-1的小方格 和i-1列放置的小方格 不重复。
• 每一列，所有连续着空着的小方格必须是偶数个

dp分析：

状态表示 f[i][j]: 前i-1列已经确定，且从第i-1列伸出的小方格在第i列的状态为j 的方案数。属性：个数。

i=2, j=11001 表示下列图的状态

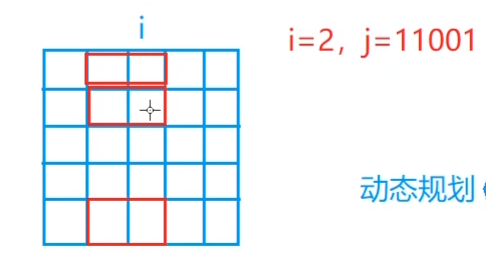
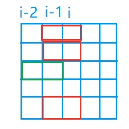
但是i-1, i列已经固定，所以集合划分是依据i-2 列伸到 i-1 列的不同状态 k 来划分

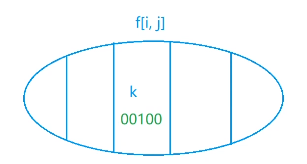
i-2 列伸到 i-1 列的状态 k=00100

状态计算：（限制条件：i-1列非空白位置可以不能放置小方格），在i列不同的放置方法就是不同的集合划分。

问题：第 i-2 列伸到 i-1 列的状态为 k ， 是否能成功转移到 第 i-1 列伸到 i 列的状态为 j ?

需要满足如下条件:

• j&k==0， i-2列伸到i-1的小方格 和i-1列放置的小方格 不重复。
• 每一列，所有连续着空着的小方格必须是偶数个

f[m][0]:
列数从0开始计数，m列不放小方格，前m-1列已经完全摆放好并且不伸出来的状态

#include<iostream>
#include<cstring>

using namespace std;

//数据范围1~11
const int N = 12;
//每一列的每一个空格有两种选择，放和不放，所以是2^n
const int M = 1 << N;
//方案数比较大，所以要使用long long 类型
//f[i][j]表示 i-1列的方案数已经确定，从i-1列伸出，并且第i列的状态是j的所有方案数
long long f[N][M];
//第 i-2 列伸到 i-1 列的状态为 k ， 是否能成功转移到 第 i-1 列伸到 i 列的状态为 j
//st[j|k]=true 表示能成功转移
bool st[M];
//n行m列
int n, m;

int main() {
//    预处理st数组
    while (cin >> n >> m, n || m) {
        for (int i = 0; i < 1 << n; i++) {
//            第 i-2 列伸到 i-1 列的状态为 k ， 
//            能成功转移到 
//            第 i-1 列伸到 i 列的状态为 j
            st[i] = true;
//            记录一列中0的个数
            int cnt = 0;
            for (int j = 0; j < n; j++) {
//                通过位操作，i状态下j行是否放置方格，
//                0就是不放， 1就是放
                if (i >> j & 1) {
//                    如果放置小方块使得连续的空白格子数成为奇数，
//                    这样的状态就是不行的，
                    if (cnt & 1) {
                        st[i] = false;
                        break;
                    }
                }else cnt++;
//                不放置小方格
            }

            if (cnt & 1) st[i] = false;
        }

//        初始化状态数组f
        memset(f, 0, sizeof f);

//        棋盘是从第0列开始，没有-1列，所以第0列第0行，不会有延伸出来的小方块
//        没有横着摆放的小方块，所有小方块都是竖着摆放的，这种状态记录为一种方案
        f[0][0] = 1;
//        遍历每一列
        for (int i = 1; i <= m; i++) {
//            枚举i列每一种状态
            for (int j = 0; j < 1 << n; j++) {
//                枚举i-1列每一种状态
                for (int k = 0; k < 1 << n; k++) {
//                    f[i-1][k] 成功转到 f[i][j]
                    if ((j & k) == 0 && st[j | k]) {
                        f[i][j] += f[i - 1][k]; //那么这种状态下它的方案数等于之前每种k状态数目的和
                    }
                }
            }
        }
//        棋盘一共有0~m-1列
//        f[i][j]表示 前i-1列的方案数已经确定，从i-1列伸出，并且第i列的状态是j的所有方案数
//        f[m][0]表示 前m-1列的方案数已经确定，从m-1列伸出，并且第m列的状态是0的所有方案数
//        也就是m列不放小方格，前m-1列已经完全摆放好并且不伸出来的状态
        cout << f[m][0] << endl;
    }
    return 0;
}