C++

$\color{#cc33ff}{— > 算法基础课题解}$

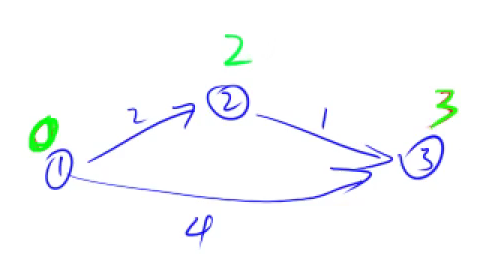
Dijkstra算法：进行n次迭代，以确定每个点到起点的距离的最小值。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 510;

int n, m;
int g[N][N]; // 稠密图，用邻接矩阵来存
int dist[N]; // 存储 当前 1号点到n号点的最短距离
bool st[N]; // 每个点的最短路是否已经确定

int dijkstra() { // 核心算法
    memset(dist, 0x3f, sizeof dist); // 初始化距离
    dist[1] = 0; // 把1号点距离初始化为0

    for (int i = 0; i < n; i ++) { // 迭代n次
        int t = -1; // 还未确定
        for (int j = 1; j <= n; j ++) // 目的：在dist还未确定的点当中，找到dist最小的一个点
            if (!st[j] && (t == -1 || dist[t] > dist[j])) // 如果当前这个点还没有确定最短路
                t = j;

        st[t] = true; // 把t加入到集合中

        for (int j = 1; j <= n; j ++) // 以t来更新其他点的距离
            dist[j] = min(dist[j], dist[t] + g[t][j]);
    }

    if (dist[n] == 0x3f3f3f3f) return -1; // 如果1和n不连通
    return dist[n]; // 否则返回最短距离
}


int main() {
    scanf("%d%d", &n, &m);

    // for (int i = 1; i <= n; i ++) // 初始化法一
    //     for (int j = 1; j <= n; j ++)
    //         if (i == j) g[i][j] = 0;
    //         else g[i][j] = 0x3f3f3f3f;
    memset(g, 0x3f, sizeof g); // 初始化法二

    while (m --) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = min(g[a][b], c); // 可能有多条边，只保留最短的
    }        

    int t = dijkstra();

    printf("%d", t);
    return 0;
}