C++

$\color{#cc33ff}{— > 算法基础课题解}$

思路：

拓扑排序

$关于拓扑排序：$

1.拓扑排序的概念

设有 a,b,c,d 等事情，其中 a 有最高优先级，b,c 优先级相同，d 是最低优先级，表示为 a -> (b, c) -> d，那么 abcd 或 acbd 都是可行的排序。把事情看成图的点，把先后关系看成有向边，问题转换为在图中求一个有先后关系的排序，这就是拓扑排序。如下图一。
显然，一个图能进行拓扑排序的充要条件是它是一个有向无环图。有环图不能进行拓扑排序。

2.图的入度和出度

拓扑排序需要用到点的入度和出度的概念。
出度：以点 u 为起点的边的数量称为 u 的出度。（或者说：这个点，它有几条指向外面的边）
入度：以点 v 为终点的边的数量称为 v 的入度。（或者说：这个点，有几条边指向它）

一个点的入度和出度体现了这个点的先后关系。如果一个点的入度等于0，则说明它是起点，是排在前面的；如果它的出度等于0，则说明它是排在后面的。例如下图二中，点 a、c的入度为0，它们都是优先级最高的事情；d 的出度为0，它的优先级最低。

图一：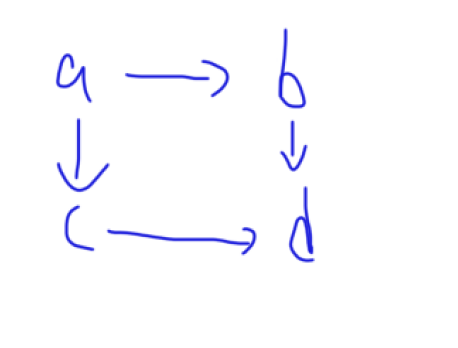

图二：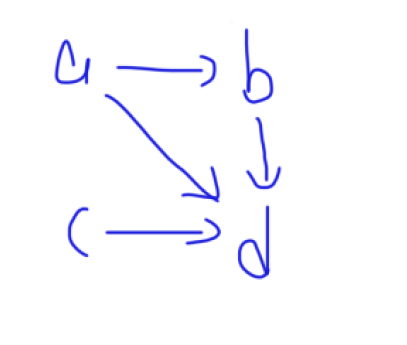

$code1:$

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1e5 + 10;

int n, m;
int h[N], e[N], ne[N], idx;
int q[N], d[N]; // q:队列，d:点的入度

void add (int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

bool topsort() {
    int hh = 0, tt = -1; // 定义队头队尾

    for (int i = 1; i <= n; i ++) {
        if (!d[i])
        q[++tt] = i; // 将所有入度为0的点插入到队列中
    }

    while (hh <= tt) {
        int t = q[hh ++]; // 取出队头

        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i]; // 找到出边
            d[j] --; // 让入度--
            if(d[j] == 0) q[++ tt] = j;
        }
    }

    return tt == n - 1; 
    // 如果 tt = n - 1,说明所有点都进队列了，那么它就是一个有向无环图，否则说明它是存在环的一个图
}

int main() {
    cin >> n >> m;
    memset(h, -1, sizeof h); // 初始化

    for (int i = 0; i < m; i ++) {
        int a, b;
        cin >> a >> b;
        add(a, b); // 建边
        d[b] ++; // a 指向 b, b的入度 +1
    }

    if (topsort()) {
        for (int i = 0; i < n; i ++) cout << q[i] << ' ';
    }
    else cout << "-1";
    return 0;
}

$code2:$

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int n, m;
int h[N], e[N], ne[N], idx;
int q[N], d[N];

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

bool topsort() {
    int hh = 0, tt = -1;

    for (int i = 1; i <= n; i ++)
        if (!d[i])
            q[++ tt] = i;

    while (hh <= tt) {
        int t = q[hh ++];

        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            d[j] --; 
            if (d[j] == 0) q[++ tt] = j;
        }
    }  

    return tt == n - 1;
}

int main() {
    cin >> n >> m;

    memset(h, -1, sizeof h);
    for (int i = 0; i < m; i ++) {
        int a, b; cin >> a >> b;
        add(a, b);
        d[b] ++;
    }

    if (topsort()) {
        for (int i = 0; i < n; i ++) cout << q[i] << ' ';
    }
    else puts("-1");

    return 0;
}