C++

$\color{#cc33ff}{— > 算法基础课题解}$

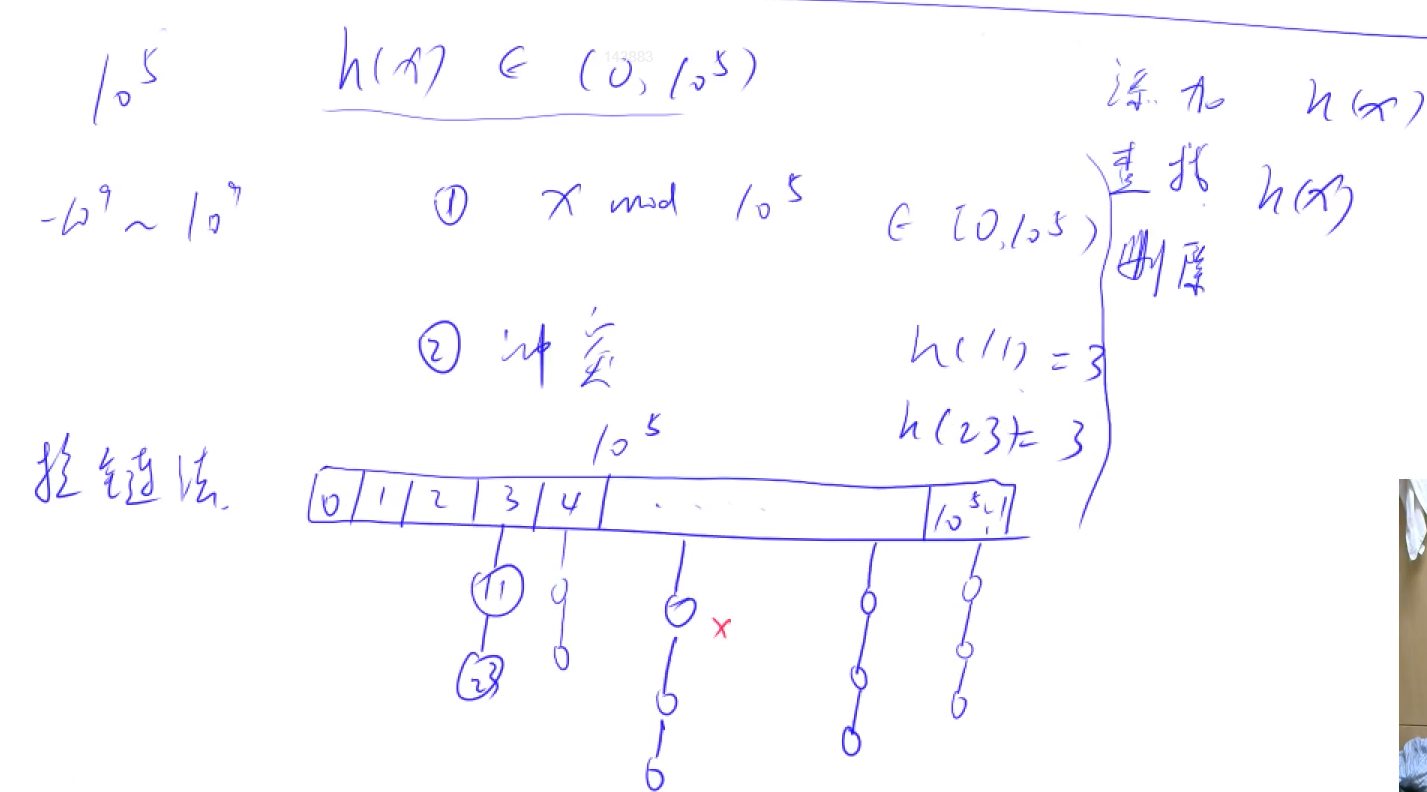
拉链法

$图解：$

#include <iostream>
#include <cstring>
using namespace std;

const int N = 1e5 + 3; // 大于1e5的第一个质数，这样取质数冲突的可能性最小

int h[N], e[N], ne[N], idx;
//h:槽，e:每个槽上的链的元素的值，ne:下一个位置在什么地方
int n;

//拉链法

//插入操作
void insert (int x) {
    int k = (x % N + N) % N; // 把x映射一个从0 ~ N之间的一个数
    e[idx] = x; //存值
    ne[idx] = h[k];
    h[k] = idx ++;
}

//查询操作
bool find (int x) {
    int k = (x % N + N) % N; // 把x映射一个从0 ~ N之间的一个数
    for (int i = h[k]; i != -1; i = ne[i]) {
        if (e[i] == x) // 如果找到
        return true;
    }
    return false;//没有找到
}

int main(){
    cin >> n;

    memset(h, -1, sizeof h); // 初始化，空指针一般用-1来表示
    while (n -- ) {
        char op[2];
        int x;
        scanf ("%s%d", op, &x);

        if (op[0] == 'I') insert (x);
        else {
            if (find (x)) cout << "Yes" << endl;
            else cout << "No" << endl;
        }
    }
    return 0;
}

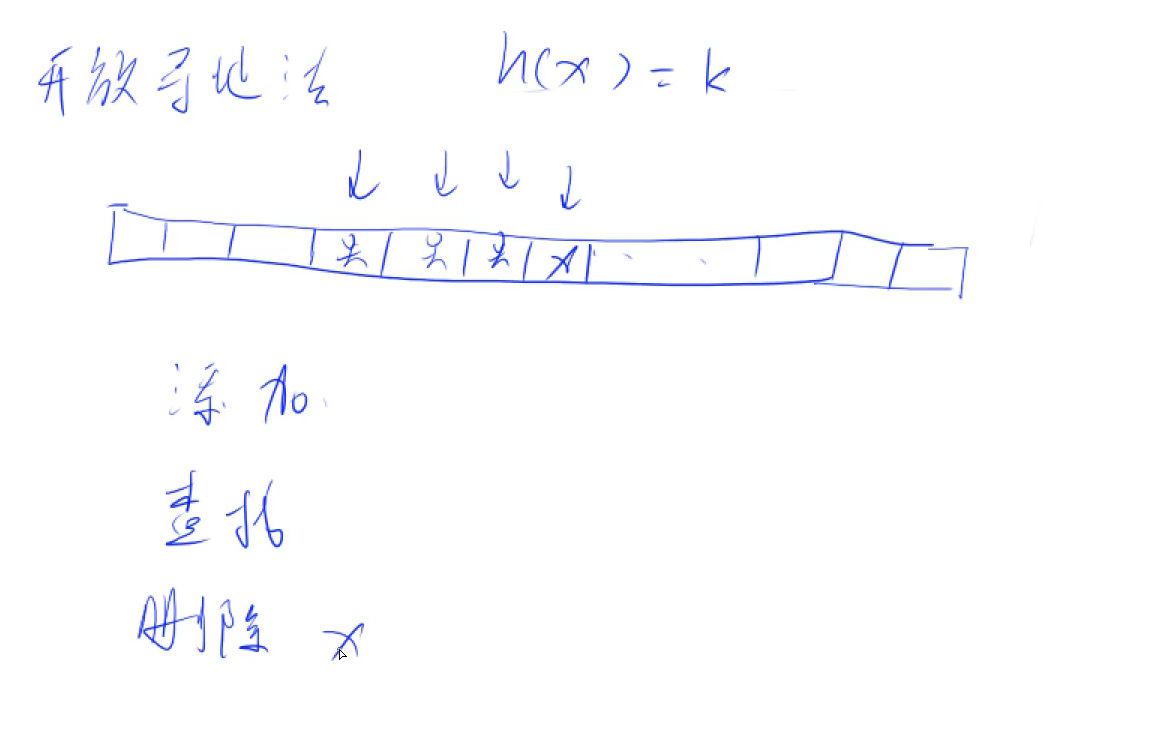
开放寻址法

$图解：$

#include <iostream>
#include <cstring>
using namespace std;

const int N = 2e5 + 3, null = 0x3f3f3f3f; // 大于2e5的第一个质数，这样取质数冲突的可能性最小

int h[N];
int n;

//开放寻址法

// 如果x在哈希表中，返回x的下标；如果x不在哈希表中，返回x应该插入的位置
int find (int x) {
    int k = (x % N + N) % N; // 把x映射一个从0 ~ N之间的一个数

    while (h[k] != null && h[k] != x){ // 如果这个位置有人，并且不是x
        k ++; // 往下走
        if (k == N) k = 0; // 如果已经看到最后了，循环看第一个位置
    }
    return k;
}

int main(){
    // for (int i = 200000; ; i ++){ // 查找大于2e5的第一个质数
    //     bool flag = true;
    //     for (int j = 2; j * j <= i; j ++){
    //         if (i % j == 0){
    //             flag = false ;
    //         }
    //     }
    //     if (flag) {
    //         cout << i << endl;
    //         break;
    //     }
    // }

    cin >> n;

    memset(h, 0x3f, sizeof h); // 初始化

    while (n -- ) {
        char op[2];
        int x;
        scanf ("%s%d", op, &x);

        int k = find (x);
        if (op[0] == 'I') {
            h[k] = x;
        } 
        else {
            if (h[k] != null) cout << "Yes" << endl;
            /*
            起始时h函数的所有元素被初始化为了null,
            如果数x在散列表中出现过,那么find (x) 返回x在散列表中的下标
            并且此时h[find(x)] = x,不是等于null
            如果数x在散列表中没有出现过,那么find (x) 返回x在散列表中的应该插入的位置
            此时h[find(x)] 还是等于null,因为之前数x没有被插入过
            */
            else cout << "No" << endl;
        }
    }
    return 0;
}