C++

$\color{#cc33ff}{— > 算法基础课题解}$

$图解分析：$

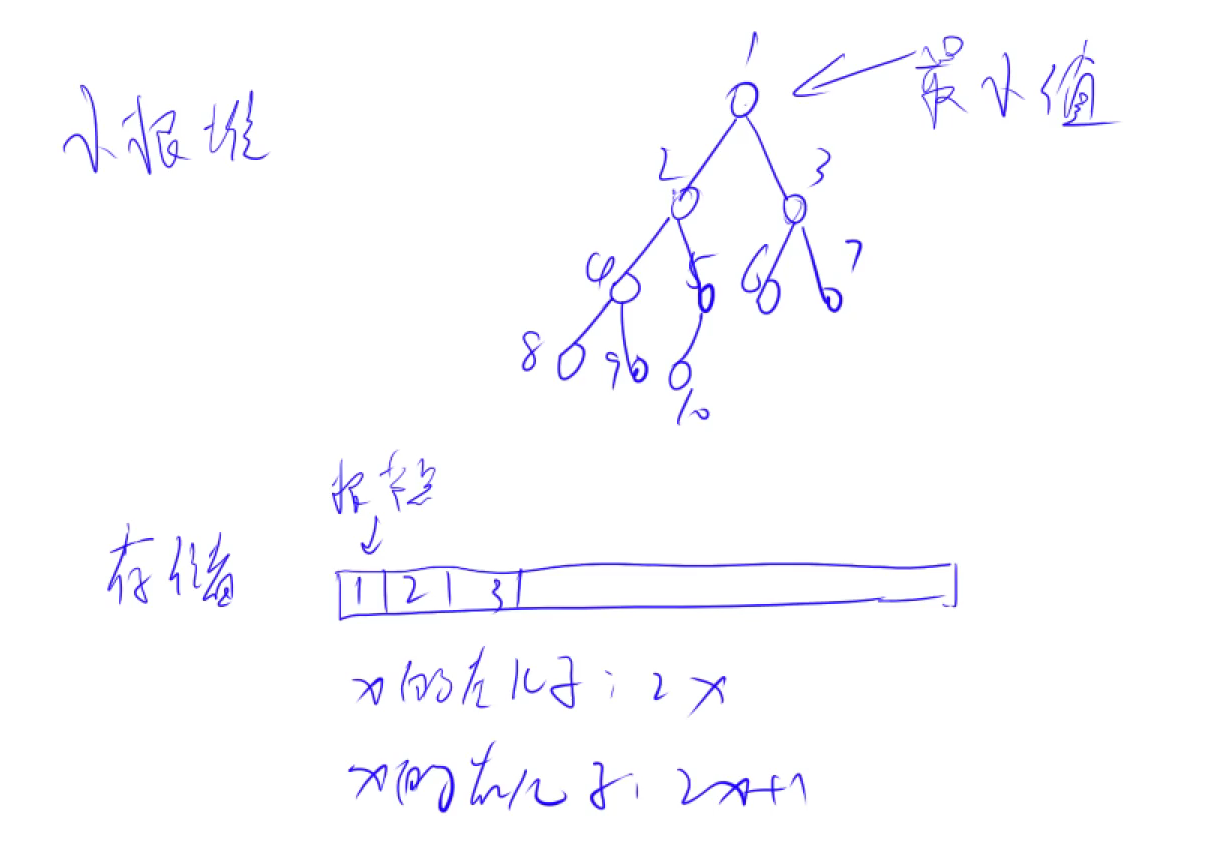
down操作：

down(u)：如果此时堆顶u不是u，u的左儿子，u的右儿子这三个点中的最小值，让u下沉

up操作：

up(u)：如果此时左儿子u比父节点小，让u上升

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1e5 + 10;

int n, m;
int h[N], size1;
// h[N]存储堆中的值, h[1]是堆顶，x的左儿子是2x, 右儿子是2x + 1, size存储当前堆中有多少元素

//down操作
void down (int u) {
    int t = u; //让t表示三个点的最小值
    if (u * 2 <= size1 && h[u * 2] < h[t]) t = u * 2; //如果左儿子存在并且小于h[t],更新t
    if (u * 2 + 1 <= size1 && h[u * 2 + 1] < h[t]) t = u * 2 + 1;//如果右儿子存在并且小于h[t],更新t

    if (u != t) {
        swap (h[u], h[t]);
        down (t);
    }
}

//up操作
void up (int u) {
    while (u / 2 && h[u / 2] > h[u]) {//如果u的父节点存在并且父节点大于u
        swap (h[u / 2], h[u]); //交换
        u /= 2; //上升
    }
}
int main(){
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) cin >> h[i];
    size1 = n;

    for (int i = n / 2; i; i --) down(i);//建堆，时间复杂度O(n)
    while (m --) {
        cout << h[1] << ' ';//输出堆顶（小根堆，堆顶元素就是整个堆的最小值）
        h[1] = h[size1]; //让堆顶被最后一个元素覆盖
        size1 --; //把最后一个元素消去
        down(1);//让堆顶归位（让堆顶变为最小值）
    }
    return 0;
}