Floyd使用场景：

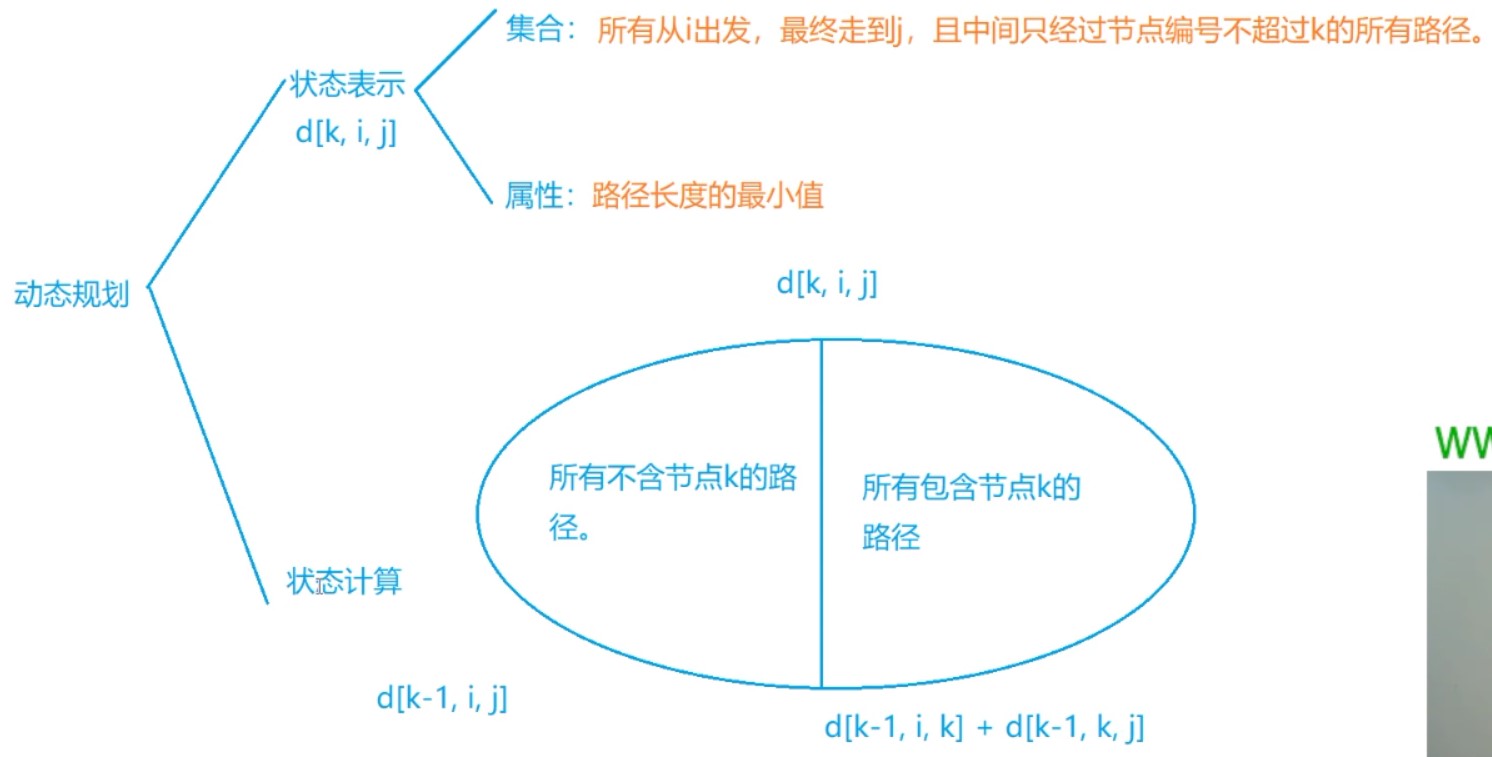
Floyd算法的DP分析法与优化：

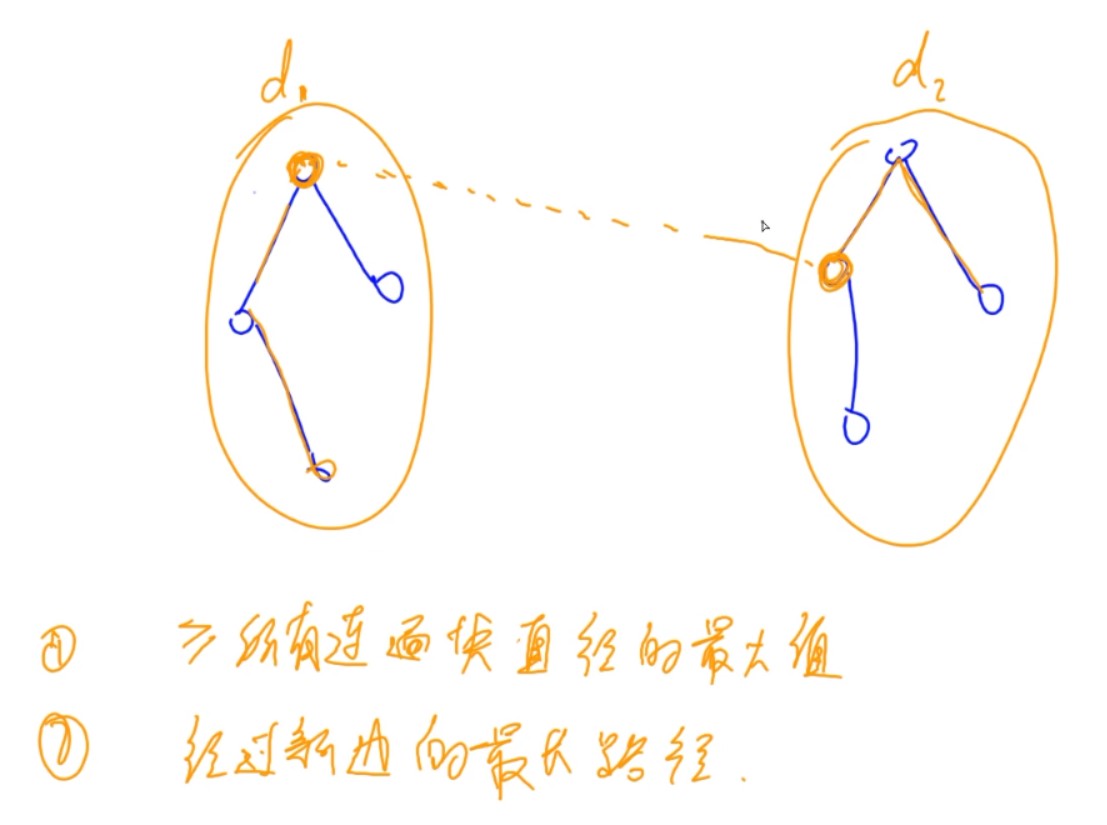
本题思路：

答案可能为：
1. 所有连通块内两个点的最长的距离（直径）。
2. 在任意两个非连通块中加一条边构成连通块的最短距离。

import java.io.*;
import java.util.*;

public class Main {
    static int N = 200;
    static double INF = 1e20; // double情况下的INF可以开大点
    static char[][] g = new char[N][N]; // 邻接矩阵
    static double[][] d = new double[N][N]; // floyd最短路
    static PII[] q = new PII[N]; // 存储每个点的x、y坐标
    static double[] maxd = new double[N]; // floyd中到每个点的最长距离

    static class PII {
        int x, y;

        public PII(int x, int y) {
            this.x = x;
            this.y = y;
        }
    }

    public static double get_dist(PII a, PII b) {
        double y = b.y - a.y, x = a.x - b.x; // 负数在下面平方后为正数

        return Math.sqrt(x * x + y * y);
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br= new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        int n = Integer.parseInt(br.readLine());
        String[] s1;

        // 坐标
        for (int i = 0; i < n; i++) {
            s1 = br.readLine().split(" ");
            q[i] = new PII(Integer.parseInt(s1[0]), Integer.parseInt(s1[1]));
        }

        // 邻接矩阵
        for (int i = 0; i < n; i++) {
            g[i] = br.readLine().toCharArray();
        }

        // floyd初始化
        for (int i = 0; i < n; i++) 
            for (int j = 0; j < n; j++) 
                if (i != j) {
                    if (g[i][j] == '1') d[i][j] = get_dist(q[i], q[j]);
                    else
                        d[i][j] = INF;
                }

        // floyd计算
        for (int k = 0; k < n; k++)
            for (int j = 0; j < n; j++)
                for (int i = 0; i < n; i++)
                    d[i][j] = Math.min(d[i][j], d[i][k] + d[k][j]);

        // 计算最短路中到每个点的最长距离
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                if (d[i][j] < INF)
                    maxd[i] = Math.max(maxd[i], d[i][j]);

        // 连通块中最长距离                    
        double res1 = 0;
        for (int i = 0; i < n; i++)
            res1 = Math.max(res1, maxd[i]);

        // 任意两个非连通块连通后的内部最短距离
        double res2 = INF;
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                if (d[i][j] >= INF) // 注意double在比较大小时的精度问题
                    res2 = Math.min(res2, get_dist(q[i], q[j]) + maxd[i] + maxd[j]);

        bw.write(String.format("%.6f\n", Math.max(res1, res2)));

        bw.flush();
    }
}