题目描述
满足6种操作:
1.插入一个数
2.删除一个数
3.查询一个数的排名
4.查询一个排名对应的值
5.查询一个数的前驱(比它小的最大数)
6.查询一个数的后继(比它大的最小数)
平衡树
平衡树是一种很特殊的二叉树。
每个点有一个权值key
一个点左子树上所有点的权值小于它自己的权值
右子树上所有点的权值大于它自己的权值
所以中序遍历一定是有序的
普通平衡树满足6种操作,也就是题目中的那6种
如果这颗平衡树是完全二叉树,也就是比较平衡的状态,
每次查询平均都是O(logn)的
但是正常插入可能会被卡掉,比如顺次插入5,4,3,2,1
就会变成这样
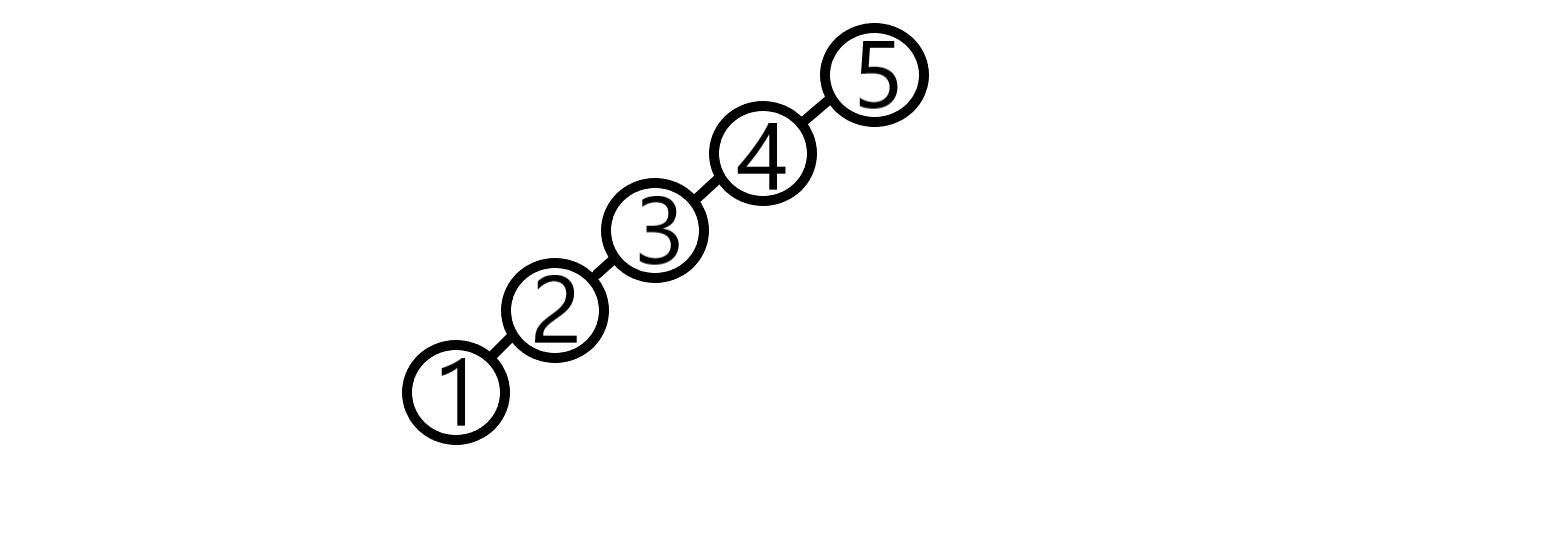
这幅图里如果一直查询1,每次查询就是O(n)的,很容易超时
但不难发现,这条链并不是该平衡树的唯一合法形态
一种更平衡的形态就是这样
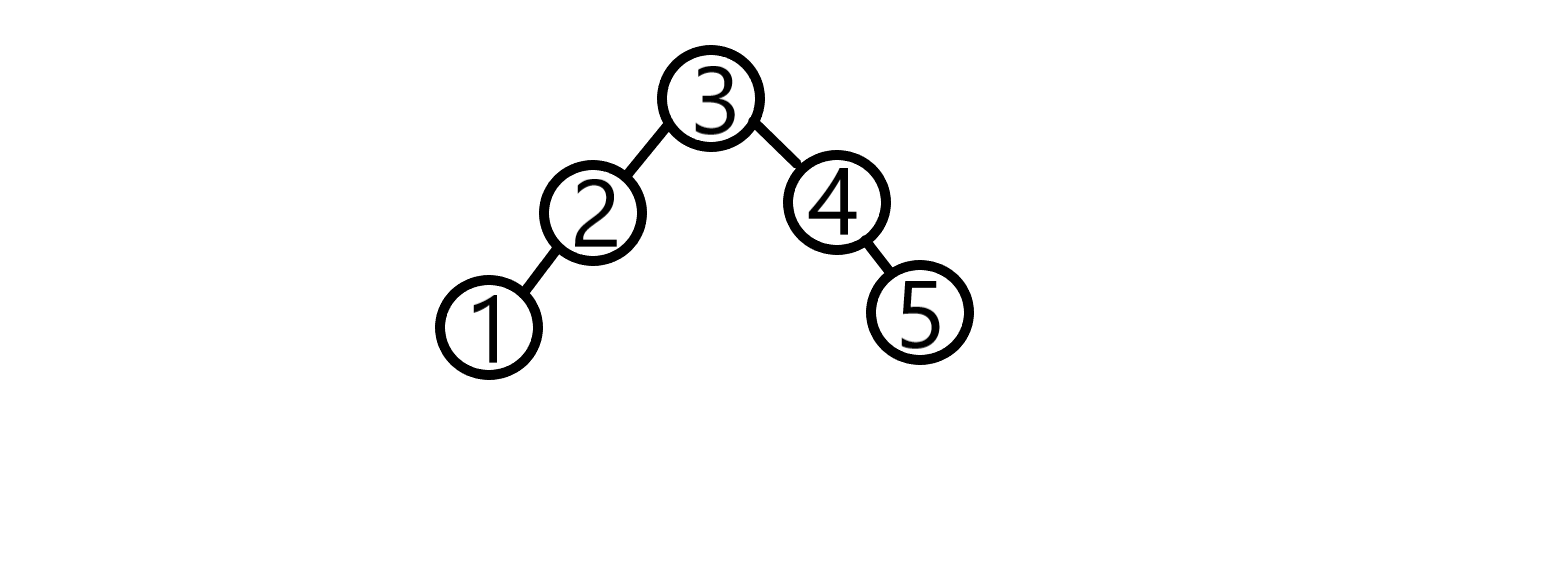
所以需要加入另一个权重,var
让它等于一个随机值(rand)
然后优先让var更大的点在上面
这样这棵树虽然不保证一定平衡,但更不容易被卡掉
(出题人:我哪知道这个rand得了个神马东西)
总结一下普通平衡树需要存多少信息
struct node{
int l,r; //左儿子和右儿子
int key,var; //两个权重
int cnt,size; //该key的数目,以及以该点为根的子树的大小(所有cnt相加)
}tr[N];
建树
一开始,我们需要建一棵“空”的平衡树
建两个哨兵
一个编号为 1,key 为 -INF
另一个编号为 2,key 为 INF
哨兵的作用主要有两个
1.方便后续插入,不需要特判第一个插入的点
2.有的题需要自动忽略大于某值或小于某值的数
这时候设置一下 INF 和 -INF 的值,如果插入时发现不在合法区域,可以直接忽略
inline void build(){ //建树
get_node(-INF); //建新点
get_node(INF);
root=1;
tr[1].r=2; //设置1的右儿子2
pushup(root);
if(tr[1].var<tr[2].var) //满足上文所说var大的在上面
zag(root);
}
由于var的存在,平衡树可能有两种基本形态

右旋和左旋
为了使树更平衡,需要改变树的形态
接下来考虑如何在不改变中序遍历的情况下改变树的结构
于是右旋(zig)和左旋(zag)就诞生了!
inline void zig(int &p){ //右旋
int q=tr[p].l;
tr[p].l=tr[q].r;
tr[q].r=p;
p=q; //通过指针间接改变和原来的p关联的值
pushup(tr[p].r);
pushup(p); //pushup就是更新size
}
inline void zag(int &p){ //左旋
int q=tr[p].r;
tr[p].r=tr[q].l;
tr[q].l=p;
p=q; //通过指针间接改变和原来的p关联的值
pushup(tr[p].l);
pushup(p); //更新size
}
画两幅图就会明白
右旋的作用是把一个点整到原位置的右子树上去
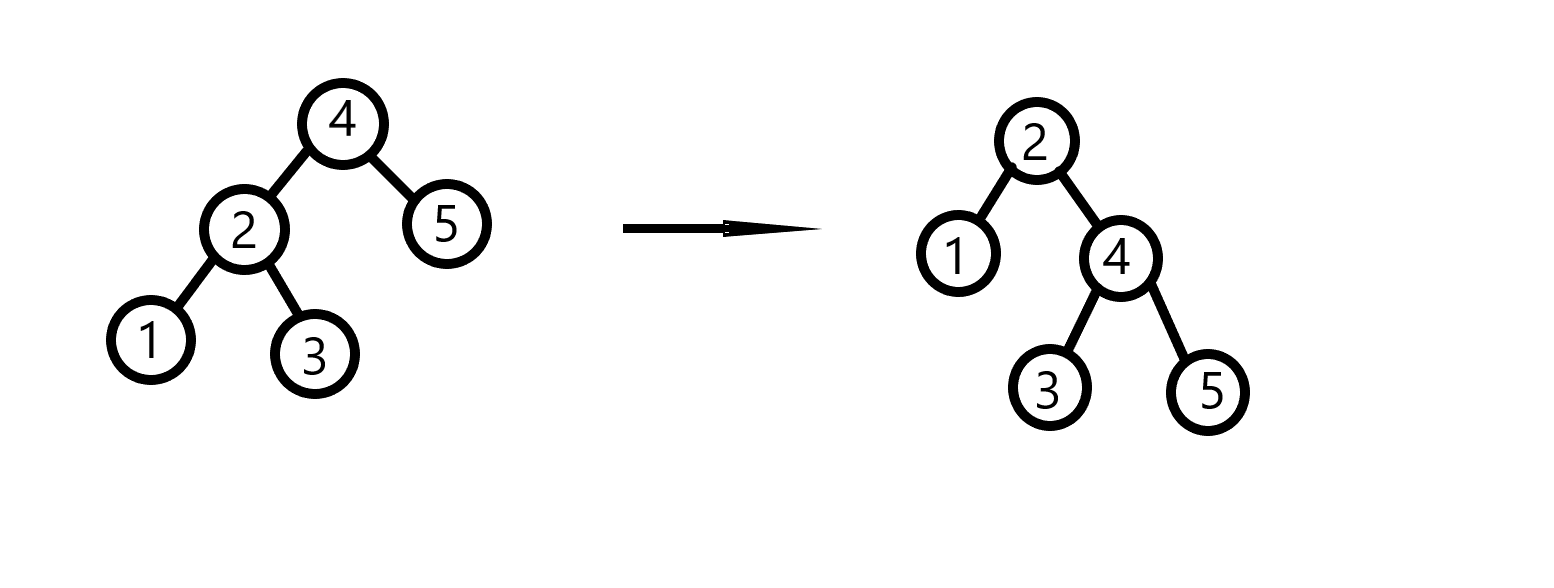
两个形态的中序遍历都是12345
同理,左旋就是右旋的反操作(把一个点整到原位置的左子树上去)
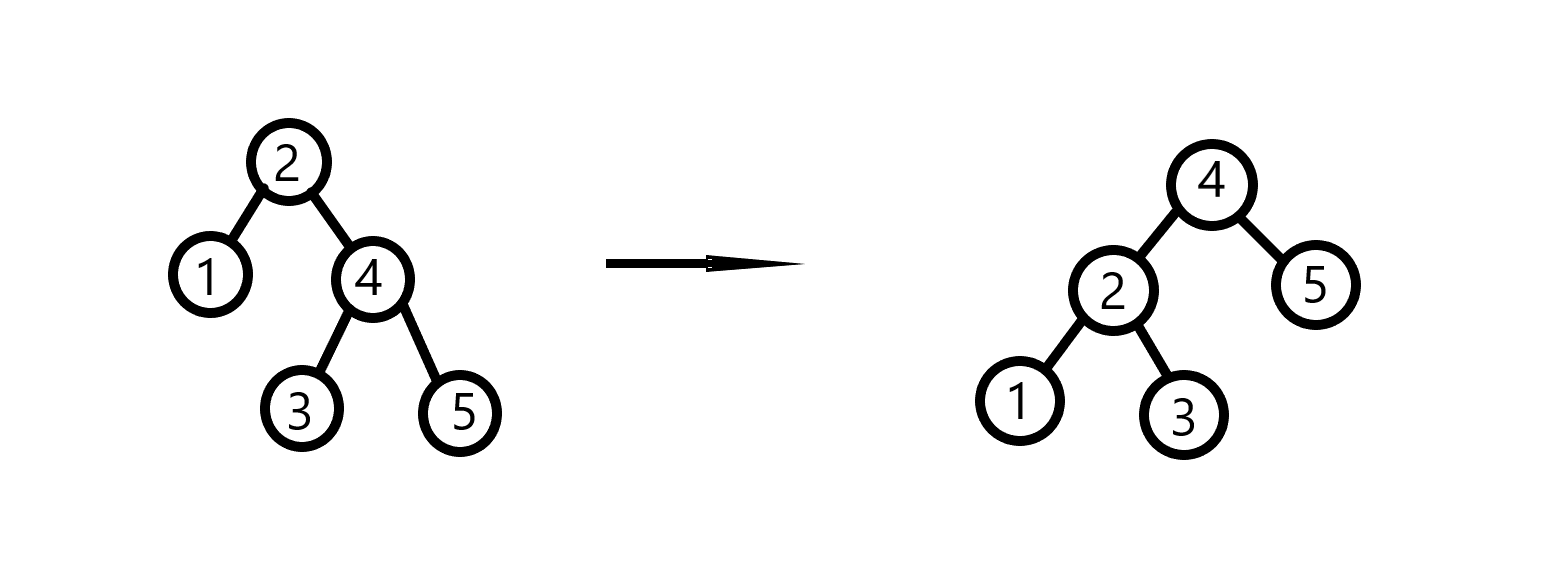
插入
由递归来实现
设置当前点为p,待插入权值为key
需要分类讨论:
1.p=0(该点不存在)
新建一个点
2.tr[p].key=key(当前点权值与待插入权值相等)
cnt+1
3.tr[p].key>key
递归到左子树
4.tr[p].key<key
递归到右子树
void insert(int &p,int key){
if(!p)
p=get_node(key); //通过指针间接设定l或r
else if(tr[p].key==key)
tr[p].cnt++;
else if(tr[p].key>key){
insert(tr[p].l,key);
if(tr[tr[p].l].var>tr[p].var) //满足var大的在上面
zig(p);
}
else{
insert(tr[p].r,key);
if(tr[tr[p].r].var>tr[p].var) //满足var大的在上面
zag(p);
}
pushup(p); //维护size
}
删除
如果删除了一个非叶子节点,左子树和右子树会不再连通,是行不通的
(其实也可以把左子树和右子树重新插入,但代码会更长)
所以只能直接删除叶子节点
如果要删除的是非叶子节点,怎么办呢?
右旋&左旋:你当我们是饭桶吗?
旋下去就行了!
同理,也是分类讨论,过程省略
void erase(int &p,int key){
if(!p) //不存在的话皆大欢喜,直接return
return;
if(tr[p].key==key) //要删除的就在这里
if(tr[p].cnt>1) //有多个,删一个即可
tr[p].cnt--;
else if(tr[p].l||tr[p].r) //有左子树或右子树
if(!tr[p].r||tr[tr[p].l].var>tr[tr[p].r].var){ //先删var大的(玄学理论)
zig(p);
erase(tr[p].r,key);
}
else{
zag(p);
erase(tr[p].l,key);
}
else //是叶子节点
p=0;
else if(tr[p].key>key) //递归到下面
erase(tr[p].l,key);
else
erase(tr[p].r,key);
pushup(p); //维护size
}
用权值求排名和用排名求权值
也是递归,过程中累加计数,看看就成了
int get_rank_by_key(int p,int key){
if(!p) //点不存在
return 0;
if(tr[p].key==key)
return tr[tr[p].l].size+1; //习惯上来讲排名从1开始,要加1
if(tr[p].key>key)
return get_rank_by_key(tr[p].l,key); //左子树的话直接返回就成
return tr[tr[p].l].size+tr[p].cnt+get_rank_by_key(tr[p].r,key);
//右子树的话要累加
}
int get_key_by_rank(int p,int rank){
if(!p) //点不存在
return 0;
if(tr[tr[p].l].size>=rank) //在左子树上
return get_key_by_rank(tr[p].l,rank);
if(tr[tr[p].l].size+tr[p].cnt>=rank) //在这个点
return tr[p].key;
return get_key_by_rank(tr[p].r,rank-tr[tr[p].l].size-tr[p].cnt); //右子树要改变排名
}
求前驱和后继
又㕛叒叕是递归,都懒得讲了
int get_prev(int p,int key){
if(!p) //前驱不存在
return -INF;
if(tr[p].key>=key) //左子树
return get_prev(tr[p].l,key);
return max(tr[p].key,get_prev(tr[p].r,key)); //右子树或本身
}
int get_next(int p,int key){
if(!p) //后继不存在
return INF;
if(tr[p].key<=key) //右子树
return get_next(tr[p].r,key);
return min(tr[p].key,get_next(tr[p].l,key)); //左子树或本身
}
完整代码
#include<iostream>
using namespace std;
const int N=100010,INF=1e8;
struct node{
int l,r;
int key,var;
int cnt,size;
}tr[N];
int root,idx;
inline void pushup(int p){ //更新大小
tr[p].size=tr[tr[p].l].size+tr[tr[p].r].size+tr[p].cnt;
}
inline int get_node(int key){ //建点
tr[++idx].key=key;
tr[idx].var=rand();
tr[idx].cnt=tr[idx].size=1;
return idx;
}
inline void zig(int &p){ //右旋
int q=tr[p].l;
tr[p].l=tr[q].r;
tr[q].r=p;
p=q;
pushup(tr[p].r);
pushup(p);
}
inline void zag(int &p){ //左旋
int q=tr[p].r;
tr[p].r=tr[q].l;
tr[q].l=p;
p=q;
pushup(tr[p].l);
pushup(p);
}
inline void build(){ //建树
get_node(-INF);
get_node(INF);
root=1;
tr[1].r=2;
pushup(root);
if(tr[1].var<tr[2].var)
zag(root);
}
void insert(int &p,int key){
if(!p)
p=get_node(key); //通过指针间接设定l或r
else if(tr[p].key==key)
tr[p].cnt++;
else if(tr[p].key>key){
insert(tr[p].l,key);
if(tr[tr[p].l].var>tr[p].var)
zig(p);
}
else{
insert(tr[p].r,key);
if(tr[tr[p].r].var>tr[p].var)
zag(p);
}
pushup(p);
}
void erase(int &p,int key){
if(!p)
return;
if(tr[p].key==key)
if(tr[p].cnt>1)
tr[p].cnt--;
else if(tr[p].l||tr[p].r)
if(!tr[p].r||tr[tr[p].l].var>tr[tr[p].r].var){
zig(p);
erase(tr[p].r,key);
}
else{
zag(p);
erase(tr[p].l,key);
}
else
p=0;
else if(tr[p].key>key)
erase(tr[p].l,key);
else
erase(tr[p].r,key);
pushup(p);
}
int get_rank_by_key(int p,int key){
if(!p)
return 0;
if(tr[p].key==key)
return tr[tr[p].l].size+1;
if(tr[p].key>key)
return get_rank_by_key(tr[p].l,key);
return tr[tr[p].l].size+tr[p].cnt+get_rank_by_key(tr[p].r,key);
}
int get_key_by_rank(int p,int rank){
if(!p)
return 0;
if(tr[tr[p].l].size>=rank)
return get_key_by_rank(tr[p].l,rank);
if(tr[tr[p].l].size+tr[p].cnt>=rank)
return tr[p].key;
return get_key_by_rank(tr[p].r,rank-tr[tr[p].l].size-tr[p].cnt);
}
int get_prev(int p,int key){
if(!p)
return -INF;
if(tr[p].key>=key)
return get_prev(tr[p].l,key);
return max(tr[p].key,get_prev(tr[p].r,key));
}
int get_next(int p,int key){
if(!p)
return INF;
if(tr[p].key<=key)
return get_next(tr[p].r,key);
return min(tr[p].key,get_next(tr[p].l,key));
}
int main(){
build();
int n;
scanf("%d",&n);
while(n--){
int type,x;
scanf("%d%d",&type,&x);
if(type==1)
insert(root,x);
else if(type==2)
erase(root,x);
else if(type==3) //从0开始,要-1
printf("%d\n",get_rank_by_key(root,x)-1);
else if(type==4)
printf("%d\n",get_key_by_rank(root,x+1));
else if(type==5)
printf("%d\n",get_prev(root,x));
else
printf("%d\n",get_next(root,x));
}
return 0;
}


写得太好了,终于看会了
感谢鼓励!
大佬用什么画图?
我也想用~
就是用的Windows里的画图3D
nbbb
萌新只会用windows的“画图”
用法差不多啊