$\huge \color{orange}{成魔之路->}$ $\huge \color{purple}{算法提高课题解}$

思路：

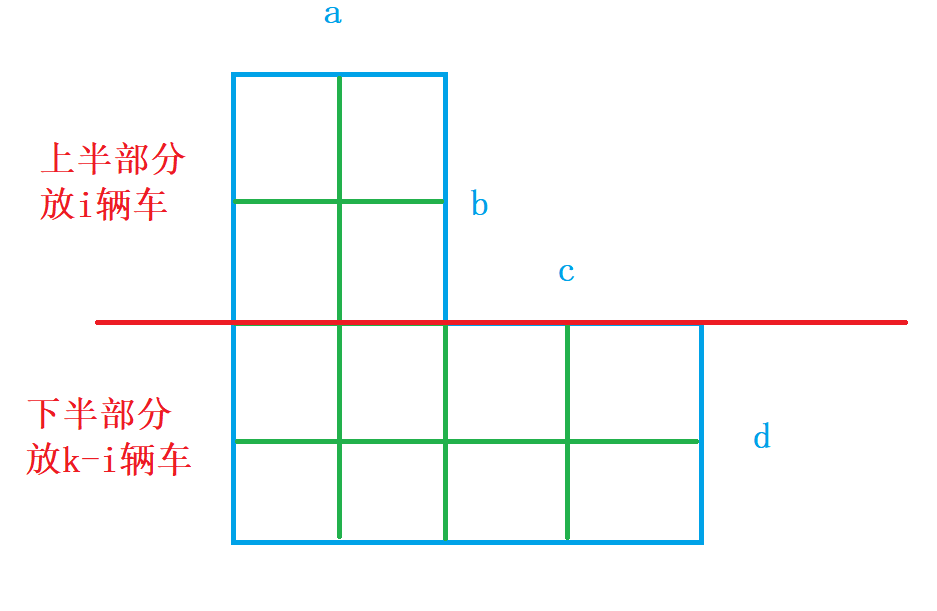
1. 将不规则图形分割成上下两个规则矩形，假设上方放 i 辆车，则下方放 k - i 辆车
2. 组合数：C(a, b) = a! / ((a - b)! * b!)；排列数：P(a, b) = a! / (a - b)!
3. 上方：C(b, i) * P(a, i)
4. 下方（注意上方列的限制）：C(d, k - i) * P(a + c - i, k - i)
5. 上方 * 下方 = C(b, i) * P(a, i) * C(d, k - i) * P(a + c - i, k - i)

完整代码

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 2010, mod = 100003;

int fact[N],infact[N];

int qmi(int a,int b)
{
    int res=1;
    while(b)
    {
        if(b&1) res=(LL)res*a%mod;
        a=(LL)a*a%mod;
        b>>=1;
    }
    return res;
}

//组合数
int C(int a,int b)
{
    if(a<b) return 0;
    return (LL)fact[a]*infact[a-b]*infact[b]%mod;
}

//排列数
int P(int a,int b)
{
    if(a<b) return 0;
    return (LL)fact[a]*infact[a-b]%mod;
}

int main()
{
    //预处理阶乘和阶乘的逆元
    fact[0]=infact[0]=1;
    for(int i=1;i<N;i++)
    {
        fact[i]=(LL)fact[i-1]*i%mod;
        infact[i]=qmi(fact[i],mod-2);
    }

    int a,b,c,d,k;
    cin>>a>>b>>c>>d>>k;

    int res=0;
    for(int i=0;i<=k;i++) res=(res+(LL)C(b,i)*P(a,i)%mod*C(d,k-i)*P(a+c-i,k-i))%mod;

    cout<<res<<endl;

    return 0;
}