<—点个赞吧QwQ

宣传一下算法提高课整理{:target=”_blank”}

小 $A$ 和小 $B$ 在玩一个游戏。

首先，小 $A$ 写了一个由 $0$ 和 $1$ 组成的序列 $S$，长度为 $N$。

然后，小 $B$ 向小 $A$ 提出了 $M$ 个问题。

在每个问题中，小 $B$ 指定两个数 $l$ 和 $r$，小 $A$ 回答 $S[l \sim r]$ 中有奇数个 $1$ 还是偶数个 $1$。

机智的小 $B$ 发现小 $A$ 有可能在撒谎。

例如，小 $A$ 曾经回答过 $S[1 \sim 3]$ 中有奇数个 $1$，$S[4 \sim 6]$ 中有偶数个 $1$，现在又回答 $S[1 \sim 6]$ 中有偶数个 $1$，显然这是自相矛盾的。

请你帮助小 $B$ 检查这 $M$ 个答案，并指出在至少多少个回答之后可以确定小 $A$ 一定在撒谎。

即求出一个最小的 $k$，使得 $01$ 序列 $S$ 满足第 $1 \sim k$ 个回答，但不满足第 $1 \sim k+1$ 个回答。

输入格式

第一行包含一个整数 $N$，表示 $01$ 序列长度。

第二行包含一个整数 $M$，表示问题数量。

接下来 $M$ 行，每行包含一组问答：两个整数 $l$ 和 $r$，以及回答 even 或 odd，用以描述 $S[l \sim r]$ 中有偶数个 $1$ 还是奇数个 $1$。

输出格式

输出一个整数 $k$，表示 $01$ 序列满足第 $1 \sim k$ 个回答，但不满足第 $1 \sim k+1$ 个回答，如果 $01$ 序列满足所有回答，则输出问题总数量。

数据范围

$N \le 10^9 , M \le 5000$

输入样例：

10
5
1 2 even
3 4 odd
5 6 even
1 6 even
7 10 odd

输出样例：

3

思路

这是一题带权并查集的题。
观察数据可发现要离散化，我们直接用一个$map$记录一下就好了。
重点是怎么算权值。
在$find$函数后的距离数组表示当前点到根的距离。
所以如果有两个点$x,y$，他们的距离是$s$，那么就像下图一样合并即可：

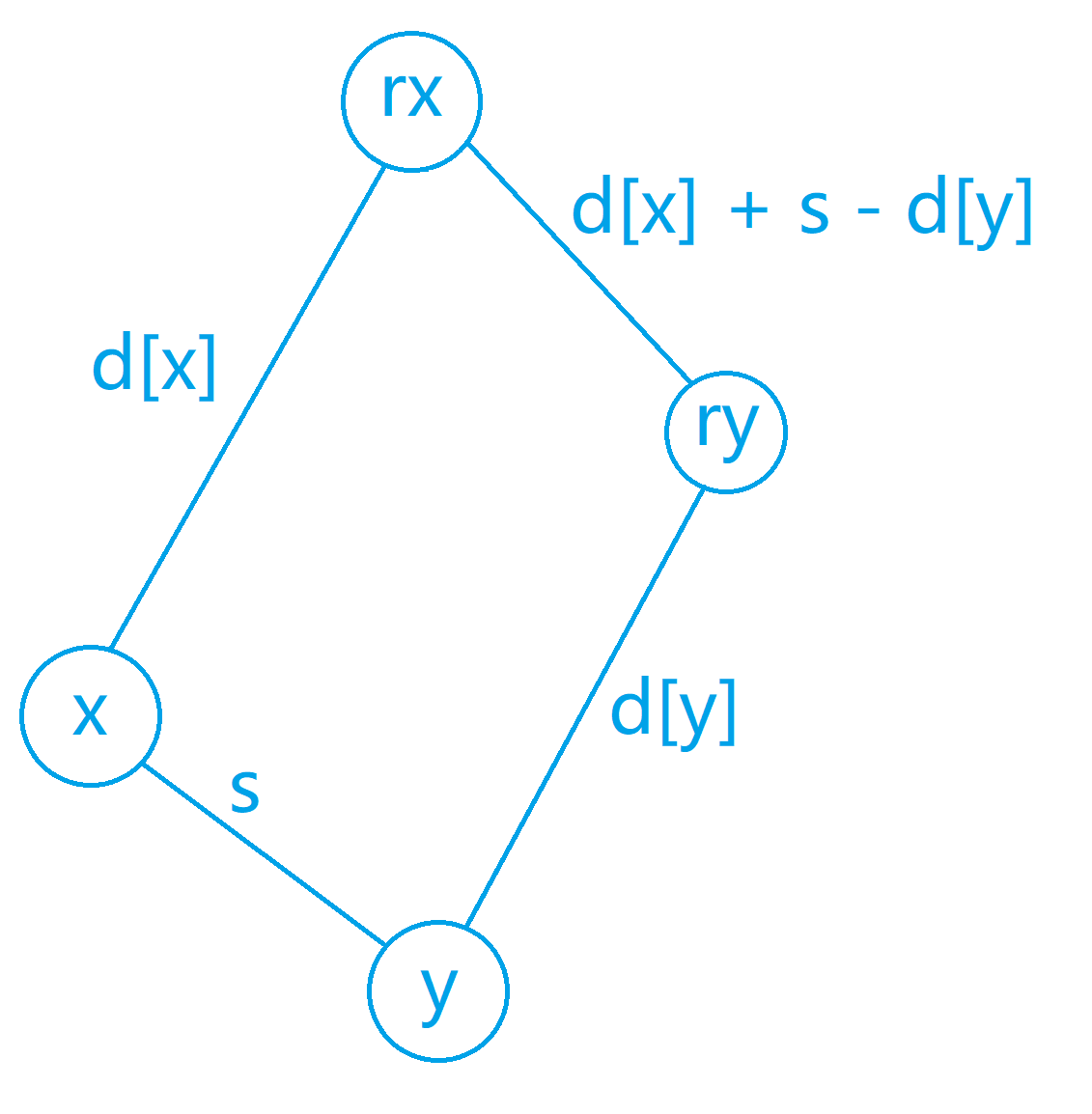
因为$y$通过两个位置来计算的结果是一样的，所以得出结论：$d[ry]=d[rx]+(s==odd)-d[y]$
在实际计算中，我们可以在最后取模。

代码

#include <iostream>
#include <unordered_map>
using namespace std;
const int N = 10010;
int n,m;
int p[N],d[N];
unordered_map <int,int> mp;
int get (int x) {
    if (!mp.count (x)) mp[x] = ++n;
    return mp[x];
}
int find (int x) {
    if (p[x] != x) {
        int rx = find (p[x]);
        d[x] += d[p[x]];
        p[x] = rx;
    }
    return p[x];
}
int main () {
    cin >> m >> m;  //n没啥用，都要离散化的
    for (int i = 1;i < N;i++) p[i] = i;
    int ans = m;
    for (int i = 1;i <= m;i++) {
        int x,y;
        string s;
        cin >> x >> y >> s;
        x = get (x - 1),y = get (y);    //这里是为了变成左开右闭的区间，因为x是要保留的，因为一减就会减掉当前数
        int rx = find (x),ry = find (y);
        int t = s == "odd";
        if (rx == ry && abs (d[x] - d[y]) % 2 != t) {
            ans = i - 1;
            break;
        }
        else if (rx != ry) {
            p[ry] = rx;
            d[ry] = abs (d[x] - d[y] - t);
        }
    }
    cout << ans << endl;
    return 0;
}