约数个数

约数个数是基于算术基本定理的。对于任意一个正数N，它分解完质因数之后的结果是：

$N =\prod \limits_{i=1}^kp_i^{a_i} = p_1^{α_1}·p_2^{α_2}· ……·p_k^{α_k}$

则它的约数个数为：$(α_1+1)·(α_2+1)·……·(α_k+1)$

证明：

N的任何一个约数d，一定也可以写成 $d =p_1^{β_1}·p_2^{β_2}· ……·p_k^{\beta_k} $ ，其中 $0<= \beta_i<=\alpha_i$

其中$\beta_i$不同，会导致约数的变化，所以N的约数个数等于$\beta_1 \sim \beta_k$的取法！

不同的取法对于不同的约数。

算术基本定理：每个数的因式分解是唯一的，因式分解不一样，这两个数就不一样。

由此可得：$\beta_1$有$0 \sim \alpha_1$，共$\alpha_1+1$种选法，$\beta_k$有$\alpha_k+1$种选法。总选法个数为$(α_1+1)·(α_2+1)·……·(α_k+1)$，等于N的约数个数！

特殊小知识：int范围内，约数最多的数约数个数为1536个

题目解析

给定 n 个正整数 $a_i$，请你输出这些数的乘积的约数个数，答案对 $10^9+7$ 取模。

取模是为了防止溢出int，或者long

思路

用map或者unodered_map存储分解之后的指数都可以，unordered_map更快一些。

代码如下

#include <iostream>
#include <algorithm>
#include <unordered_map>

using namespace std;

typedef long long LL; // 用LL表示long long，比较简便

const int mod = 1e9 + 7; // 定义mod，防止long long溢出

int main()
{
    int n;
    cin >> n;

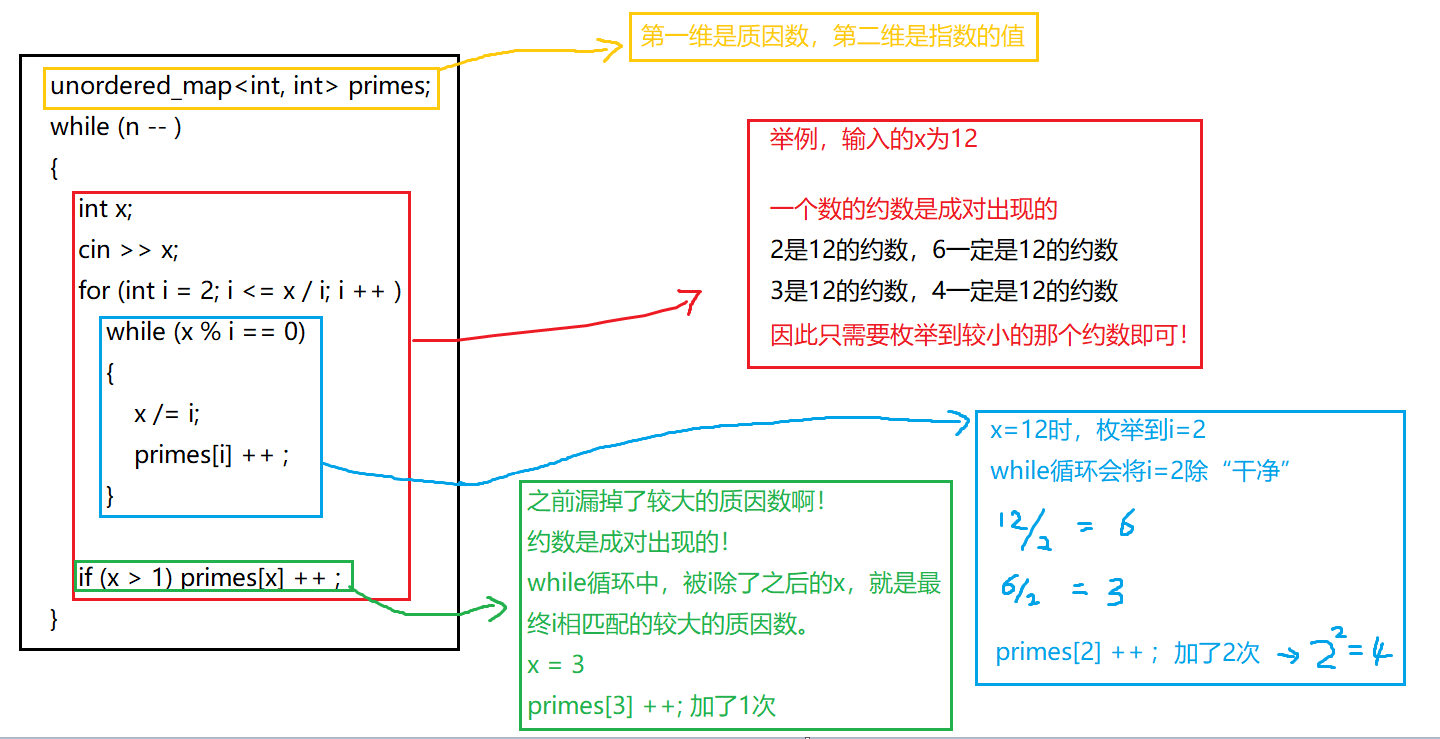
    unordered_map<int, int> primes; // 定义哈希表，第一维存储质因数，第二维存储指数
    while (n -- )
    {
        int x;
        cin >> x;
        for (int i = 2; i <= x / i; i ++ )
            while (x % i == 0) // 如果i能够整除x
            {
                x /= i; // x一直除以i，直到不能再除 
                primes[i] ++ ; // key为i的元素，value加1。此题表示因数为i的数，指数加1
            }

        if (x > 1) primes[x] ++ ; // 因数是成对存在的，现在将较大的那个因数加1
    }

    LL res = 1; // 定义答案变量
    for (auto prime : primes) res = res * (prime.second + 1) % mod; // 用约数个数公式求约数。每次都mod，防止溢出。

    cout << res << endl;

    return 0;
}

解释一下为什么这个是质因数，我刚开始出现的一个疑问(已解决)

约数之和

对于任意一个正数N，它分解完质因数之后的结果是：

$N =\prod \limits_{i=1}^kp_i^{a_i} = p_1^{α_1}·p_2^{α_2}· ……·p_k^{α_k}$

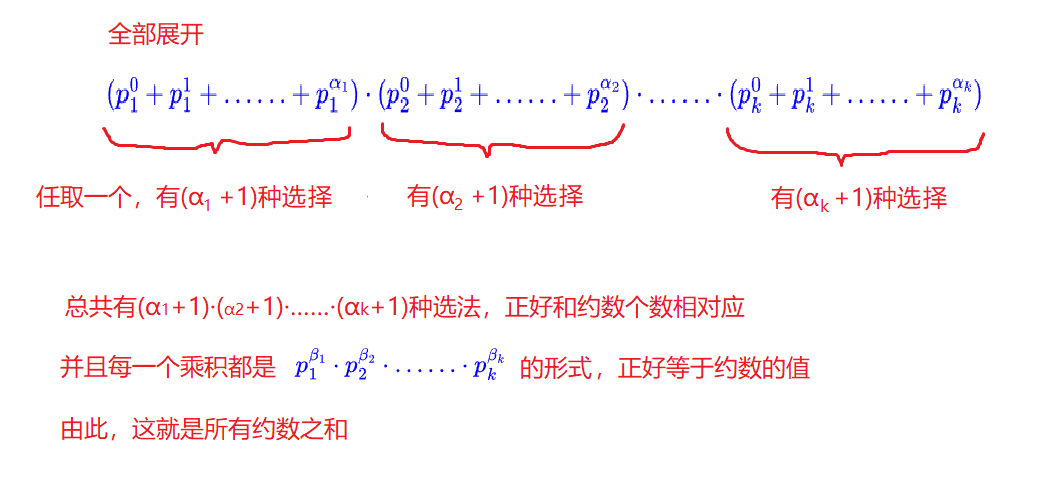
则它的约数之和为：$(p_1^0+p_1^1+……+p_1^{\alpha_1})·(p_2^0+p_2^1+……+p_2^{\alpha_2})·……·(p_k^0+p_k^1+……+p_k^{\alpha_k})$

证明：