<—点个赞吧QwQ

宣传一下算法提高课整理

司令部的将军们打算在 $N \times M$ 的网格地图上部署他们的炮兵部队。

一个 $N \times M$ 的地图由 $N$ 行 $M$ 列组成，地图的每一格可能是山地（用 H 表示），也可能是平原（用 P 表示），如下图。

在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

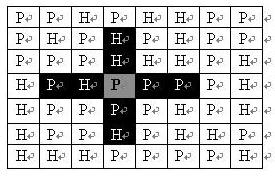
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。

图上其它白色网格均攻击不到。

从图上可见炮兵的攻击范围不受地形的影响。

现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入格式

第一行包含两个由空格分割开的正整数，分别表示 $N$ 和 $M$；

接下来的 $N$ 行，每一行含有连续的 $M$ 个字符(P 或者 H)，中间没有空格。按顺序表示地图中每一行的数据。

输出格式

仅一行，包含一个整数 $K$，表示最多能摆放的炮兵部队的数量。

数据范围

$N \le 100,M \le 10$

输入样例：

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

输出样例：

6

思路1

闫氏$\text{DP}$分析法：
状态表示：$f_{i,j,k}$

• 集合：前$i$层中，第$i-1$层状态是$j$,第$i$层状态是$k$
• 属性：$\max$

状态计算：

• 若第$i - 2$层状态是$l$，那么结果就是$f_{i - 1,l,j} + cnt_j$，其中$cnt_i$是状态$i$中放的大炮的数量
• 所以状态转移方程就是$f_{i,j,k}=\max\lbrace f_{i,j,k},f_{i - 1,l,j} + cnt_j\rbrace$

起始状态：$f_{0,0,0}$
目标状态：$f_{n + 2,0,0}$（所有第$n$层的状态都会计算到这里，可以省代码）

代码1

别抄，会错的

#include <iostream>
#include <vector>
using namespace std;
const int N = 110,M = 1 << 10;
int n,m;
int g[N];
int f[N][M][M];
int cnt[M];
vector <int> state;
bool check (int x) {
    for (int i = 0;i < m;i++) {
        if ((x >> i & 1) && ((x >> i + 1 & 1) || (x >> i + 2 & 1))) return false;
    }
    return true;
}
int count (int x) {
    int ans = 0;
    for (int i = 0;i < m;i++) ans += x >> i & 1;
    return ans;
}
int main () {
    cin >> n >> m;
    for (int i = 1;i <= n;i++) {
        for (int j = 0;j < m;j++) {
            char ch;
            cin >> ch;
            if (ch == 'H') g[i] += 1 << j;
        }
    }
    for (int i = 0;i < 1 << m;i++) {
        if (check (i)) {
            state.push_back (i);
            cnt[i] = count (i);
        }
    }
    for (int i = 1;i <= n + 2;i++) {
        for (int j = 0;j < state.size ();j++) {
            for (int k = 0;k < state.size ();k++) {
                for (int l = 0;l < state.size ();l++) {
                    int a = state[j],b = state[k],c = state[l];
                    if ((a & b) | (b & c) | (a & c)) continue;
                    if ((g[i - 1] & a) | (g[i] & b)) continue;
                    f[i & 1][j][k] = max (f[i][j][k],f[i - 1][l][j] + cnt[b]);
                }
            }
        }
    }
    cout << f[n + 2][0][0] << endl;
    return 0;
}

思路2

$\text{MLE}$了怎么办，滚动数组优化！

代码2

#include <iostream>
#include <vector>
using namespace std;
const int N = 110,M = 1 << 10;
int n,m;
int g[N];
int f[2][M][M];
int cnt[M];
vector <int> state;
bool check (int x) {
    for (int i = 0;i < m;i++) {
        if ((x >> i & 1) && ((x >> i + 1 & 1) || (x >> i + 2 & 1))) return false;
    }
    return true;
}
int count (int x) {
    int ans = 0;
    for (int i = 0;i < m;i++) ans += x >> i & 1;
    return ans;
}
int main () {
    cin >> n >> m;
    for (int i = 1;i <= n;i++) {
        for (int j = 0;j < m;j++) {
            char ch;
            cin >> ch;
            if (ch == 'H') g[i] += 1 << j;
        }
    }
    for (int i = 0;i < 1 << m;i++) {
        if (check (i)) {
            state.push_back (i);
            cnt[i] = count (i);
        }
    }
    for (int i = 1;i <= n + 2;i++) {
        for (int j = 0;j < state.size ();j++) {
            for (int k = 0;k < state.size ();k++) {
                for (int l = 0;l < state.size ();l++) {
                    int a = state[j],b = state[k],c = state[l];
                    if ((a & b) | (b & c) | (a & c)) continue;
                    if ((g[i - 1] & a) | (g[i] & b)) continue;
                    f[i & 1][j][k] = max (f[i & 1][j][k],f[i - 1 & 1][l][j] + cnt[b]);
                }
            }
        }
    }
    cout << f[n + 2 & 1][0][0] << endl;
    return 0;
}