<—点个赞吧QwQ

宣传一下算法提高课整理{:target=”_blank”}

有 $N$ 个物品和一个容量是 $V$ 的背包。

物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。

如下图所示：

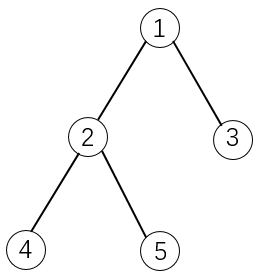
如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。

每件物品的编号是 $i$，体积是 $v_i$，价值是 $w_i$，依赖的父节点编号是 $p_i$。物品的下标范围是 $1 … N$。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式

第一行有两个整数 $N，V$，用空格隔开，分别表示物品个数和背包容量。

接下来有 $N$ 行数据，每行数据表示一个物品。
第 $i$ 行有三个整数 $v_i, w_i, p_i$，用空格隔开，分别表示物品的体积、价值和依赖的物品编号。
如果 $p_i = -1$，表示根节点。 数据保证所有物品构成一棵树。

输出格式

输出一个整数，表示最大价值。

数据范围

$1 \\le N, V \\le 100$
$1 \\le v_i, w_i\\le 100$

父节点编号范围：

• 内部结点：$1 \\le p_i \\le N$;
• 根节点 $p_i = -1$;

输入样例

5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2

输出样例：

11

思路

闫氏$\text{DP}$分析法：
状态表示：$f_{i,j}$

• 集合：以第$i$个点为根节点的子树里选且选上$i$这个点的所有总体积不超过$j$的方案
• 属性：$\max$

状态计算：

• 如果不选的话，价值就是$0$
• 如果所有儿子总体积不超过$0$，价值就是$\max\lbrace g_{son_i,0} + v_i\rbrace$（其中$g_{son_i,j}$表示$i$的所有子节点的总体积不超过$j$的所有方案）
• 如果所有儿子总体积不超过$1$，价值就是$\max\lbrace g_{son_i,1} + v_i\rbrace$
• 如果所有儿子总体积不超过$j-w_i$，价值就是$\max\lbrace g_{son_i,j-w_i} + v_i\rbrace$
• 所以状态转移方程就是$f_{i,j}=\underset{0\le k \le j-w_i}\max\lbrace g_{son_i,k} + v_i\rbrace$

代码

#include <iostream>
#include <cstring>
using namespace std;
const int N = 110,M = 110;
int n,m;
int h[N],e[N],ne[N],idx;
int w[N],v[N];
int f[N][M];
void add (int a,int b) {
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}
void dfs (int u) {
    for (int i = h[u];~i;i = ne[i]) {
        int to = e[i];
        dfs (to);
        for (int j = m - w[u];j >= 0;j--) {
            for (int k = 0;k <= j;k++) f[u][j] = max (f[u][j],f[u][j - k] + f[to][k]);
        }
    }
    for (int j = m;j >= w[u];j--) f[u][j] = f[u][j - w[u]] + v[u];
    for (int j = 0;j < w[u];j++) f[u][j] = 0;
}
int main () {
    memset (h,-1,sizeof (h));
    cin >> n >> m;
    int root = 0;
    for (int i = 1;i <= n;i++) {
        int p;
        cin >> w[i] >> v[i] >> p;
        if (~p) add (p,i);
        else root = i;
    }
    dfs (root);
    cout << f[root][m] << endl;
    return 0;
}