该题的第二问是求最少需要几个最长不上升子序列可以覆盖所有的数，解决这个问题的重点在于深入理解用贪心求最长上升子序列的做法。

代码中的f数组即为与答案有关的数组,需要放置的系统个数必须大于等于最长上升子序列的长度，不能小于。

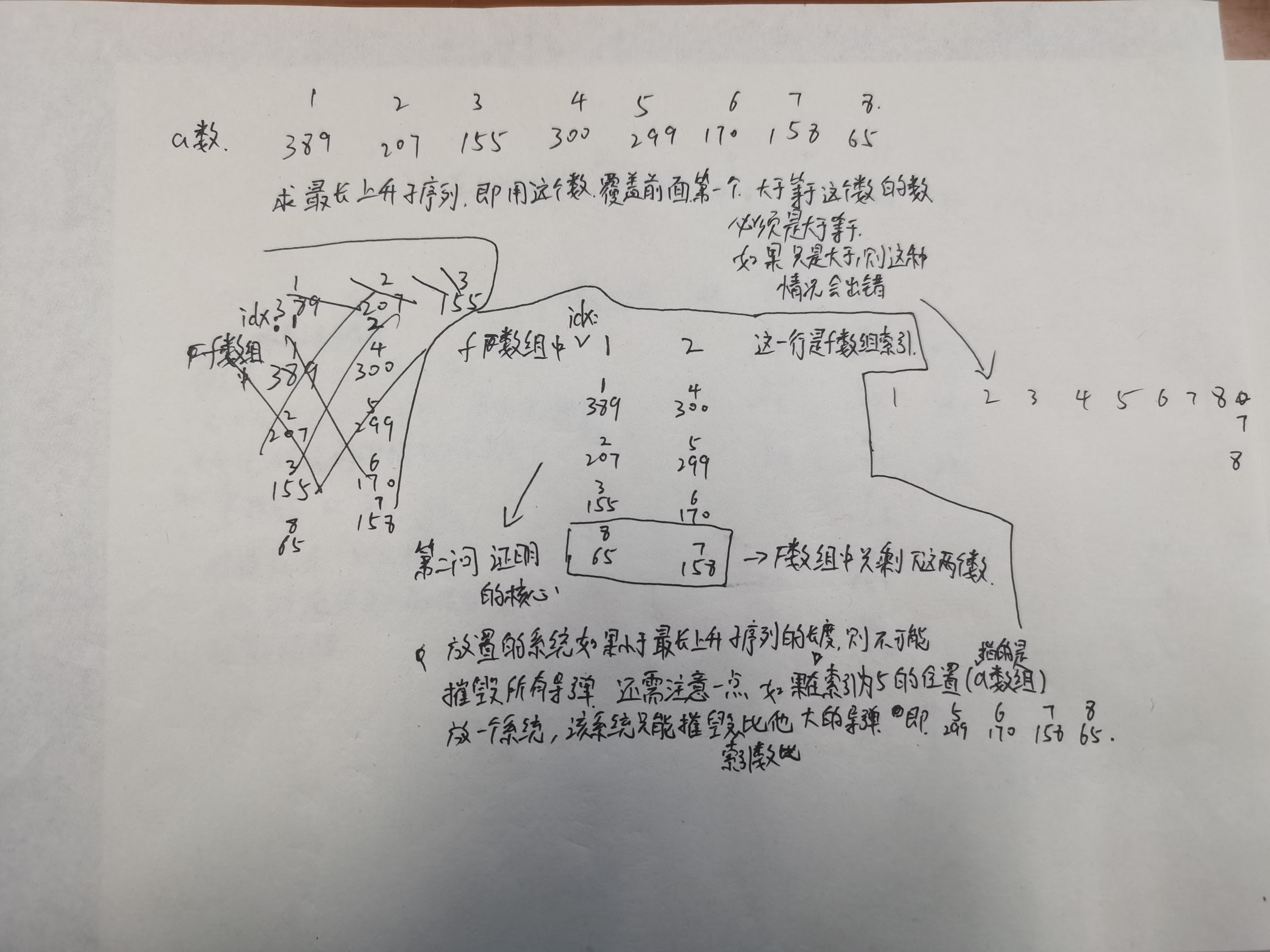
证明如下，即一个防御系统不可能同时摧毁最长上升子序列（假设有一个最长上升序列，x1,x2,x3,x4,……，xn,x1< x2<x3<……<xn）中的两个炮弹，若要同时摧毁两个炮弹，则摧毁前面一个炮弹的时候，不可能再摧毁后面的任何一个最长上升子序列中的炮弹。

下面图片证明的是为什么可以取到最长上升子序列的长度，而且索引在哪些位置放置可以达到条件

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1e5 + 10;

int a[N], f[N];

int main()
{
    int x,cnt = 0;
    while (~scanf("%d", &x)) a[ ++ cnt] = x;

    int j = 1;
    f[1] = a[1];
    for (int i = 2; i <= cnt; i ++ )
    {
        if (a[i] <= f[j]) f[++ j] = a[i];
        else
        {
            int l = 1, r = j;
            while (l < r)
            {
                int mid = l + r >> 1;
                if (f[mid] >= a[i]) l = mid + 1;
                else r = mid;
            }
            f[r] = a[i];
        }
    }

    printf("%d\n", j);
    j = 1;
    f[1] = a[1];
    for (int i = 1; i <= cnt; i ++ )
    {
        if (a[i] > f[j]) f[ ++ j] = a[i];
        else 
        {
            int l = 1, r = j;
            while (l < r)
            {
                int mid = l + r >> 1;
                if (f[mid] < a[i]) l = mid + 1;
                else r = mid;
            }
            f[r] = a[i];
        }
    }
    printf("%d\n", j);
    return 0;
}