题目描述

给你 n 个非负整数 $a_1$，$a_2$，…，$a_n$，每个数代表坐标中的一个点($i$, $a_i$) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 ($i$, $a_i$) 和 ($i$, $0$)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

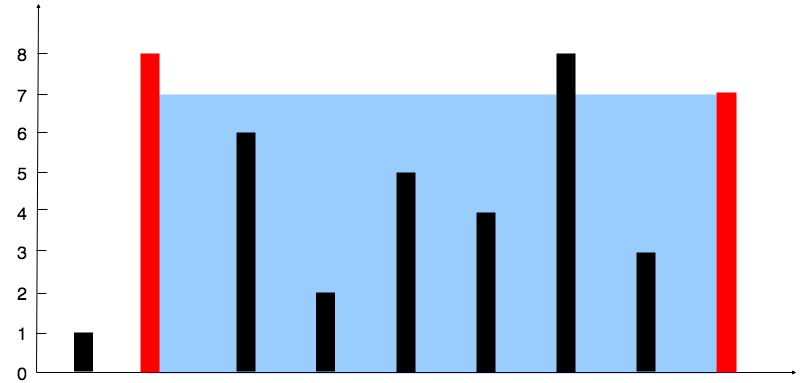
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例：

输入：[1,8,6,2,5,4,8,3,7]
输出：49

算法思路

1. 暴力枚举

• 为了找到两条直线，使其所围成面积最大，我们可以通过两层暴力循环枚举，找出所有可能的直线的组合，计算其面积，并找到最大值，时间复杂度为$O(n^2)$.
• C ++代码如下，但是时间会爆掉。

class Solution {
public:
    int maxArea(vector<int>& height) {
        int res = 0;
        for (int i = 0; i < height.size(); i ++)
            for (int j = i + 1; j < height.size(); j ++)
                res = max(res, min(height[i], height[j]) * (j - i));

        return res;
    }
};

2. 双指针法

在暴力解法中，每固定一条直线，就要遍历剩下的所有直线，造成了大量元素的多次重复访问。那么我们有没有办法只扫描一次数组，就可以找到最大的面积呢？让我们来看看双指针算法是怎么做的。

• 最开始的时候，如果我们用指针i和j指向最两端的直线，此时两条直线之间的距离就是最大的，即我们所求矩形面积的宽度(width)为最大。
• 但是位于最两端的直线不一定是最高的，所以它们组成矩形的面积也就不一定是最大的。因此我们依然需要继续遍历整个数组，这时我们将指向数组两端的指针慢慢往里面收敛，直到找到面积最大值。
• 对于此时i和j指向的直线，他们之间的宽度已经是最宽了。于是在收敛的过程中，如果遇到的高度比两端的柱子更低的话，由于之间的宽度更短，所以面积必定更小，我们就可以直接跳过，不予考虑。我们只需要考虑收敛时出现的那些高度更高的柱子。
• 该方法在双指针向中间收敛的过程中，对数组中的每个元素只访问了一次，因此时间复杂度为O(n).

C ++代码

class Solution {
public:
    int maxArea(vector<int>& height) {
        int i = 0, j = height.size() - 1;
        int res = 0;
        while (i < j)
        {
            int h = min(height[i], height[j]);
            res = max(res, h * (j - i));
            while (i < j && height[i] <= h) i ++;
            while (i < j && height[j] <= h) j --;
        }
        return res;
    }
};