$\huge \color{orange}{成魔之路->}$ $\huge \color{purple}{算法提高课题解}$

思路：

1. 查询：for(int i = x; i; i -= lowbit(i)) res += tr[i];
2. 修改：for(int i = x; i <= n; i += lowbit(i)) tr[i] += c;
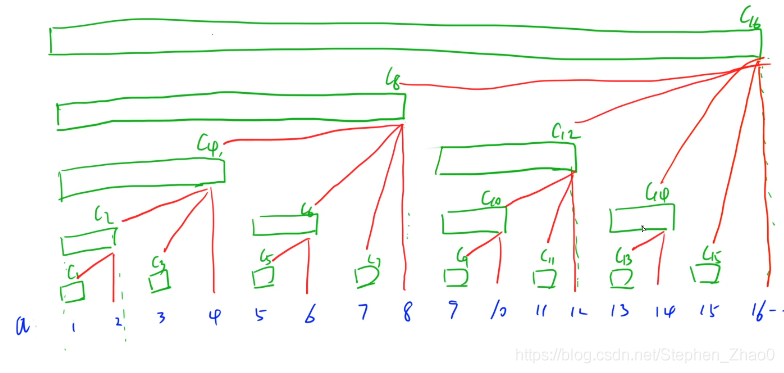
3. tr[x] 表示 [x - lowbit(x) + 1, x] 中数的个数
4. 分成 n 类，对于每一个 a[i]，找左边大于(小于) a[i] 的个数和右边大于(小于) a[i] 的个数，将两者相乘

完整代码

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 200010;

int n;
int a[N], tr[N];
int Greater[N], Lower[N];

int lowbit(int x) {
    return x & -x;
}

// 统计 1 ～ x 出现的数的个数
int sum(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

// tr[x] 表示 [x - lowbit(x) + 1, x] 中数的个数
void add(int x, int c) {
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}

int main() {
    cin >> n;

    for (int i = 1; i <= n; i++) cin >> a[i];

    // 找左边的
    for (int i = 1; i <= n; i++) {
        // 统计[a[i] + 1, n]中数的个数
        Greater[i] = sum(n) - sum(a[i]);

        // 统计[1, a[i] - 1]中数的个数
        Lower[i] = sum(a[i] - 1);

        //修改 a[i] 出现的次数
        add(a[i], 1);
    }

    memset(tr, 0, sizeof tr);

    // 找右边的
    LL res1 = 0, res2 = 0;
    for (int i = n; i; i--) {
        // v 的个数
        res1 += (LL) Greater[i] * (sum(n) - sum(a[i]));

        // ∧ 的个数
        res2 += (LL) Lower[i] * sum(a[i] - 1);

        //修改 a[i] 出现的次数
        add(a[i], 1);
    }

    cout << res1 << ' ' << res2 << endl;

    return 0;
}