图片上的插入排序代码有误

碎碎念：哎插入排序，堆排序全忘光了TVT

思路
判断是否为插入排序，若不是则为堆排序。

插入排序
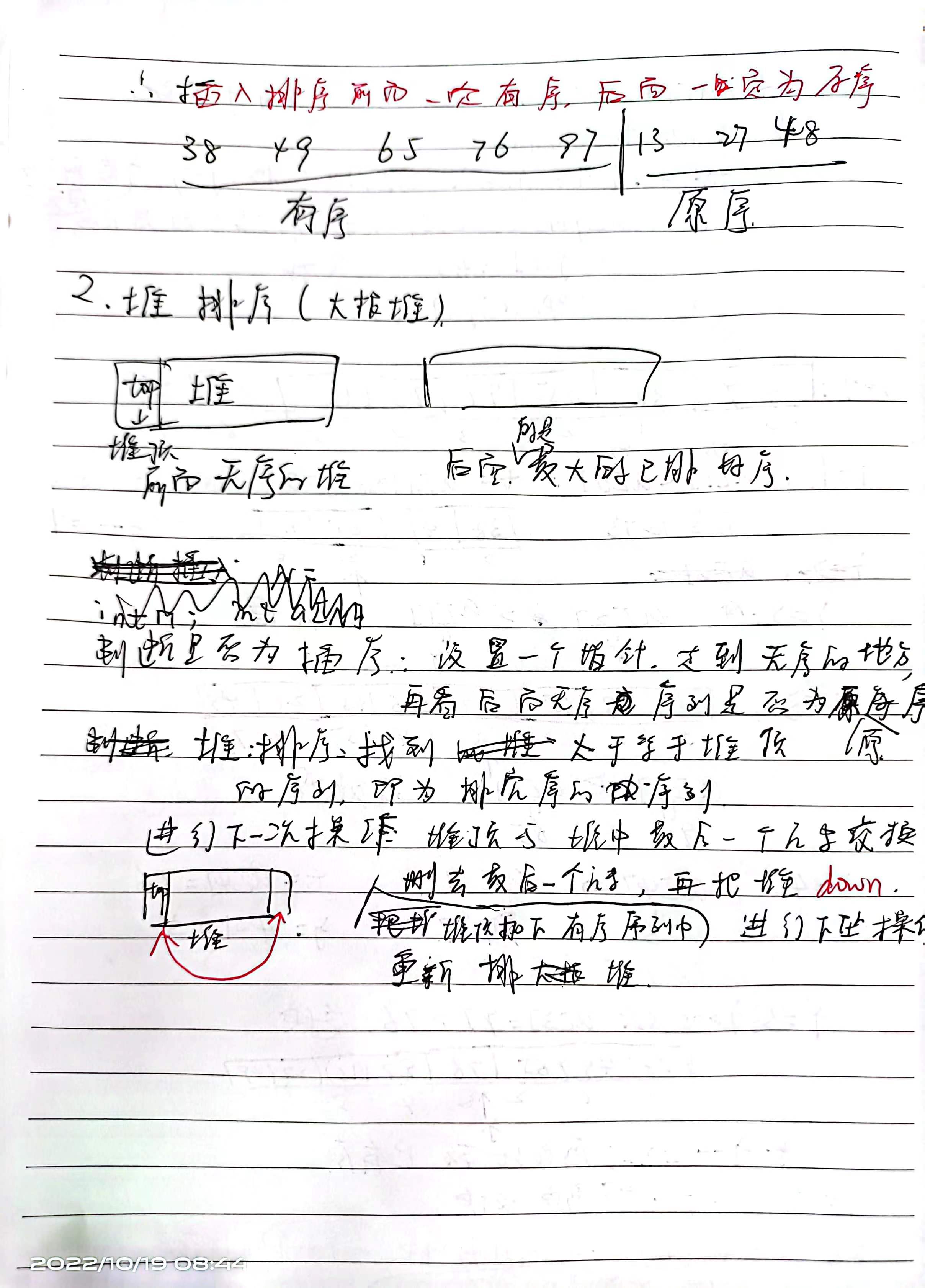
本质：看当前元素是否比前驱小，若小，则插到前面有序序列中。插入排序的前半部分都是有序的
后半部分是原序。

    ```
    void Insert(int[] a, int len)
    {
        for (int i = 1; i < len; i++)
            if (a[i] < a[i-1]) //若是比前驱小
            {
                int t = a[i];

                //前面序列中比a[i]小的元素往后移，移到剩下一个a[j]位置放a[i]
                for (int j = i-1; j >= 0 && a[j] >t && j--) 
                    a[j+1] = a[j];
                a[j+1] = t; //当前元素放到前面有序序列的正确位置中
            }
    }
    ```

堆排序
堆是前面无序，后面有序，是>= 堆顶的元素。
所以只需从后往前看，找到< 堆顶的元素，就是分界线。然后将堆顶与堆底互换，
下坠（重新对堆排序）的同时删去堆底，堆底就在有序的序列中了。

小根堆下坠代码

int h[N];
void down(int u, int size) //u为当前根节点, size为堆的大小
{
    int t = u; //t 保存的是父节点，左右孩子中的最小节点

    if (u*2 <= size && h[u*2] < h[t])  //若左孩子存在且左孩子值小，更新t
        t = u*2;
    if (u*2+1 <= size && h[u*2+1] < h[t]) //若右孩子存在且右孩子值小，更新t
        t = u*2+1;

    if (u != t) //若根节点不是最小的节点
    {
        //交换并下坠
        swap(h[t], h[u]);  
        down(t, size);
    }
}

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int a[N], b[N];
int n;

void down(int u, int size) //大根堆的下坠
{
    int t = u; //保存最大节点
    if (u*2 <= size && b[u*2] > b[t]) t = u*2; //若左孩子存在且最大，更新t
    if (u*2+1 <= size && b[u*2+1] > b[t]) t = u*2+1; //右孩子存在且最大，更新t

    if (t != u)
    {
        swap(b[u], b[t]);
        down(t, size);
    }
}

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) cin >> b[i];

    //从第二个元素开始，先判断是否为插入排序
    //前面是从小到大的有序序列，后面则无序
    int p = 2; 
    while (p <= n && b[p] >= b[p-1]) //判断前面是否有序
        p++;
    int k = p; //记录p走到哪了，k 就是无序的第一个元素
    while (p <= n && a[p] == b[p]) //判断后面是否为原序
        p++;
    if (p == n+1) //若整个走完就是插入排序
    {
        puts("Insertion Sort");

        //执行一次插入排序，只需要将b[k]插到前面的有序序列中
        while (k > 1 && b[k] < b[k-1]) //当至少有一个元素存在时
            swap(b[k-1], b[k]), k--; 
    }

    else //否则为堆排序
    {
        puts("Heap Sort");

        //从末尾出发，找到堆底
        k = n;
        while (k >= 1 && b[k] >= b[1]) k--;
        swap(b[k], b[1]); //交换堆顶，堆底
        down(1, k-1); //下坠，并删去堆底
    }

    //注意末尾无空格
    cout << b[1]; 
    for (int i = 2; i <= n; i++) cout << ' ' << b[i];

    return 0;
}